問 題
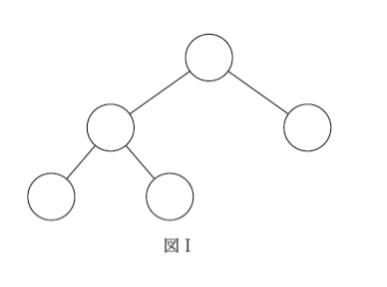
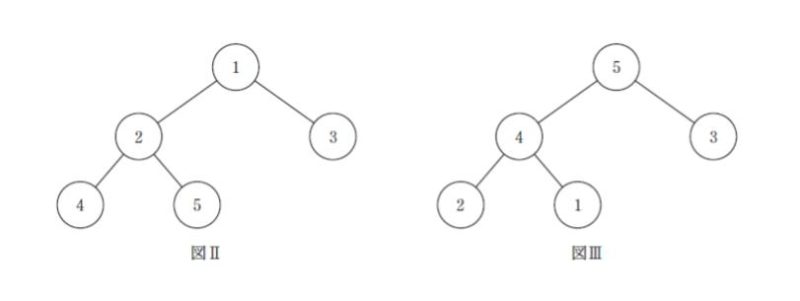
図Ⅰのような 2 分木の節それぞれに、重複しないように1 ~ 5 の整数を無作為に格納した。このとき,この2 分木がヒープである確率はいくらか。ただし,図Ⅰの2 分木において,ヒープとは,どの節の値もその子の節の値より小さいものであるとする。例えば,図Ⅱの2 分木はヒープであり,図Ⅲの2 分木はヒープではない。
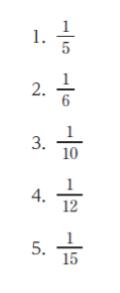
正解 (5)
解 説
ヒープの定義より、一番上の親に 5 は入りません。また、4も入りません。さらに、3も入りません。次の子に 2,1 しか使えないからです。そして、2も入りません。1の置き場がなくなるからです。つまり、一番上は 1 と決まります。
ケース1)1の左下が2→ all OK 3,4,5 の入り方が 3! = 6 通り存在
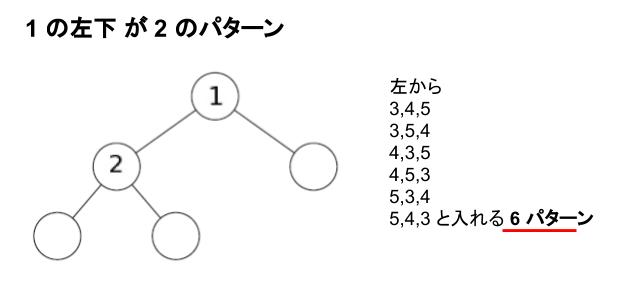
ケース2) 1 の左下が 3 → 3 の子ノード2つにおいて、4,5 の入れ替わりのみ許されるため 2 通り存在
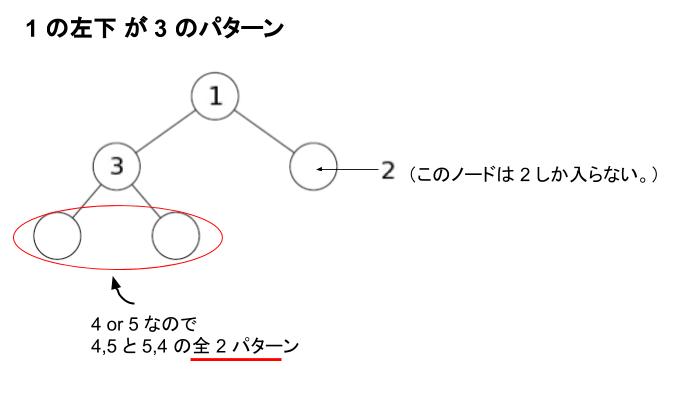
合わせて8 通りです。全通りは 5 つの数字の並びなので 5! = 120 通りです。従って、求める確率は 8/120 = 1/15 です。
以上より、正解は 5 です。
類題 H29no39

コメント