問 題
あるクラスの生徒60 人の和食，洋食，中華料理に対するし好について，次のことが分かっているとき，確実にいえるのはどれか。ただし，各生徒は， 3 種類の料理について，「好き」又は「好きでない」のいずれかであるものとする。
○ 洋食が好きでない人は，和食が好きでない。
○ 中華料理が好きでない人は，洋食が好きである。
○ 和食が好きな人は，26 人である。
○ 洋食が好きでない人は，18 人である。
○ 和食と中華料理のいずれも好きでない人は， 4 人である。
1．中華料理が好きな人は，56 人である。
2．和食と中華料理のいずれも好きな人は，22 人である。
3．洋食が好きで中華料理が好きでない人は，30 人である。
4．和食，洋食，中華料理のいずれも好きな人は， 8 人である。
5．洋食と中華料理のいずれも好きで，和食が好きでない人は，12 人である。
解 説
３つの項目について、好きか嫌いかなので、ベン図で考えます。
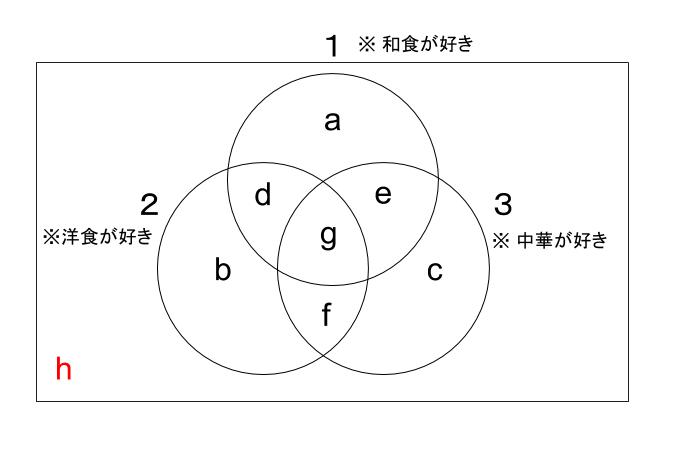
好きを◯、好きでないを☓と表します。各条件を式にしていきます。
全部で 60 人なので
a+b+c+d+e+f+g+h = 60 です。
洋食☓なら、和食☓なので、洋食☓かつ和食◯の部分である a,e は 0 です。
同様に、中華☓なら、洋食が好きなので、中華☓かつ洋食☓である a,h は 0 です。
a = e = h = 0 とまとめることができます。
和食◯が 26 人なので
a + d + e + g = 26 です。 a=e=0 なので、結局
d + g = 26 です。
洋食☓が 18 人なので
a + c + e + h = 18 です。a=e=h=0 なので、結局
c = 18 です。
和食 ☓ かつ中華 ☓ が 4 人なので
b + h = 0 です。h=0 なので、結局
b = 4 です。
わかった文字について、「全部で 60 人」の式に代入すると
0+4+18+d+0+f+g+0 = 60 なので
d + f + g = 38 となります。ここで、和食◯＝26人の式から d + g = 26 より
f = 12 とわかります。これは正に選択肢 5 の記述の内容です。
以上より、正解は 5 です。
コメント