問 題
図のような立方体の各辺の中点を結んでできる立体があり,ある正三角形の面と,これに相対する正三角形の面が灰色に塗られている。
この立体の展開図として最も妥当なのは,次のうちではどれか。
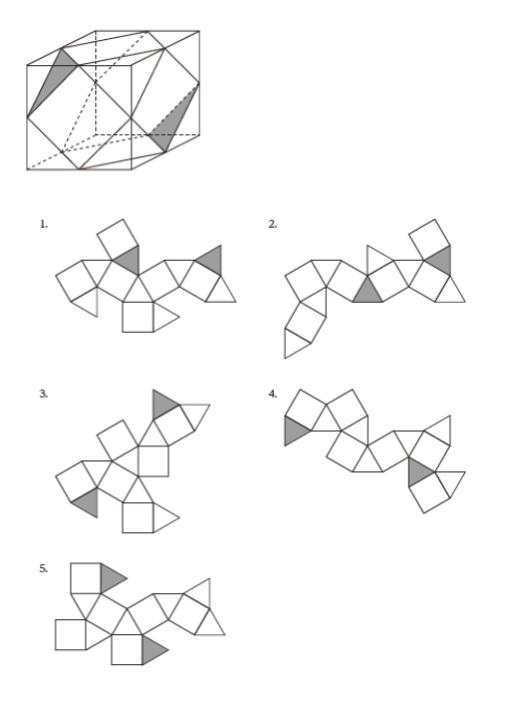
正解 (2)
解 説
展開図の問題なので「最小の角をなす2辺はくっつく。ぺりぺりちぎってくっつけてもOK。」です。
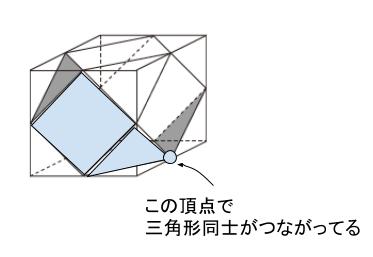
図に注目すると、灰色の三角形の辺 → 四角形の平行な辺を挟む → 三角形(頂点)と灰色の三角形(頂点)が共有 というつながりになるはずです。
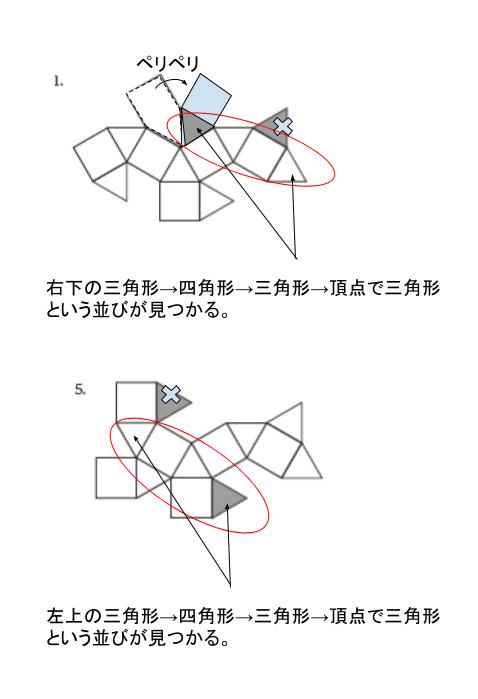
まず、選択肢 1ですが
以下のようにちぎって灰色同士を近づけると、妥当ではないと判断できます。赤丸で囲った部分の両端が平行と考えられます。
また、選択肢 5 は、そのままの展開図で判断できます。
選択肢 3,4 もペリペリはがして三角形同士を近づけると判断しやすいと思います。
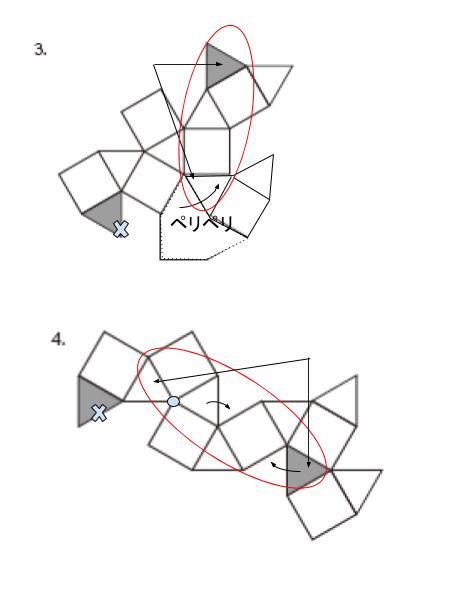
以上より、正解は 2 です。

コメント