問 題
長さ L の一次元井戸型ポテンシャル
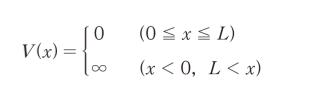
の中で質量mの粒子が自由に運動している。この粒子のエネルギーに関する次の記述の㋐、㋑に当てはまるものの組合せとして最も妥当なのはどれか。ただし、記述中の[ ]は表記を伏せていることを示す。
「この粒子のエネルギーEは、シュレーディンガー方程式を解くことで求められるが次のような方法でも導くことができる。粒子と波の二重性から、井戸型ポテンシャル中の粒子は定常波として振る舞う。定常波の波長を λ とすると
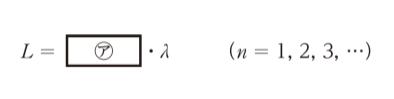
という関係を満たす場合に限り、定常波は存在する。一方、ド・ブロイの式

を用いて E を表すと
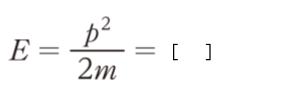
となり、シュレーディンガー方程式を解いて得られる E と等しくなる。」
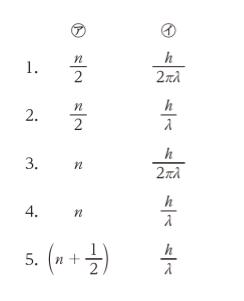
正解 (2)
解 説
定常波は、同じ波が逆方向から2つ向かってきた時に合成してできる「その場でみょんみょん動く波」です。すると、x = 0 の所と x = L の所では(境界条件より)ちょうど 変位は 0 でなくてはいけません。
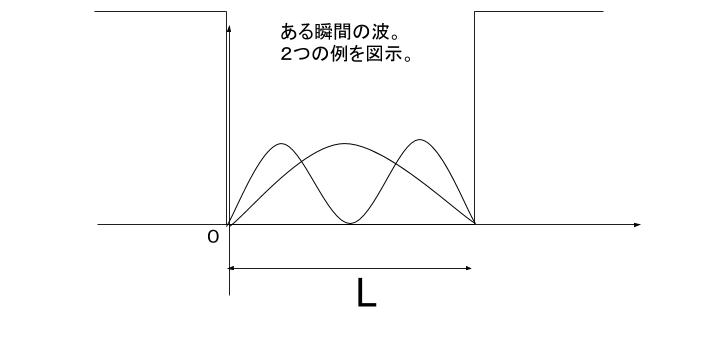
ということは、L = 1/2 λ や λ、、、ということになります。よって、㋐は n/2 です。
㋑については知識になります。
h = pλ です。p = h/λ となります。
以上より、正解は 2 です。
類題 H24no18

コメント