公務員試験 H29年 国家一般職(化学) No.1解説

　問 題　　　　　

半径が 5 の球に内接する、底面の半径が 4 の直円柱の体積として正しいのはどれか。

1．32π
2．48π
3．64π
4．80π
5．96π

 

 

 

 

 

　解 説　　　　　

【解法１　立体なので切断して考える】
立体なので、対称性を保つようにど真ん中で真っ二つに切断して切断面を考えると下図のようになります。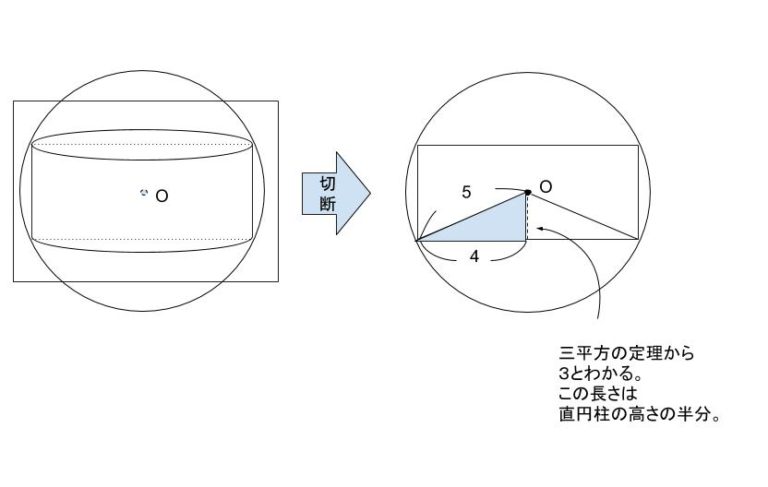

直円柱の高さは 6 とわかります。底面積は 半径 4 の円なので、16πです。従って、体積は 16 π × 6 = 96π です。

以上より、正解は 5 です。
 
【解法 2  大雑把な体積評価と選択肢の活用】
球の体積の公式は V = 4/3 πr³ です。ここで π≒3 と近似すれば、大体球の体積は 4×5³ = 500 です。図より、球の半分以上を直円錐が占めていると考えられるため体積は250以上と評価できます。

選択肢の数はだんだん大きくなっており、選択肢 4 で近似して 240 であるため、正解は 5 と考えられます。

以上より、正解は 5 です。