問 題
幅 2 m の一様な長方形断面水路を流量 25 m3/s の水が流れている。次の ㋐,㋑,㋒ のうち流れの状態が射流であるものを全て挙げているのはどれか。
ただし,断面平均流速を v,水深を H,重力加速度の大きさを 10 m/s2 とするとき,フルード数 Fr は次式で与えられるものとする。
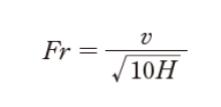
㋐ 水深が 2.0 m のとき
㋑ 水深が 2.5 m のとき
㋒ 水深が 3.0 m のとき
1.㋐
2.㋐,㋑
3.㋑
4.㋑,㋒
5.㋒
解 説
液体の流速と、波の速度 の関係に注目して流れを分類することがあり、この時、流れを「常流」と「射流」に大別します。
常流は、流速が波速よりも遅い流れのことです。
射流は、流速が波速よりも速い流れのことです。
2つの流れを同時に見ることができる身近な例が、台所のシンクです。水道の水を流した時に、水が落ちる場所近くは 流速 > 波速 で「射流」が見られます。
一方、水が落ちる場所からやや離れると波面が見られる「常流」が観測されます。射流 → 常流 の際に「跳水」が見られることも確認できると思われます。
常流か射流か、というのは流速 v と波速 c:√gH の比 である「フルード数:v/√gH」に注目することで判別できます。Fr < 1 なら 常流、Fr > 1 なら 射流です。
※ Fr = 1 の時は、常流でも射流でもありません。限界流と呼ばれます。
㋐ ですが
Q = Av なので、25 = 2 × 2.0 v です。v = 6.25 m/s です。フルード数の分母は √10 × 2.0 = √20 ≒ 4.5 です。Fr = 6.25/√20 ≒ 6.25/4.5 > 1 です。Fr > 1 より 射流です。㋐ が射流なので、正解は 1 or 2 です。
㋑ ですが
Q = Av なので、25 = 2 × 2.5 v です。v = 5 m/s です。フルード数の分母は √10 × 2.5 = √25 = 5 です。Fr = 5/5 = 1 です。フルード数がちょうど1なので、限界流です。限界流は、常流でも射流でもないため、㋑ は射流ではありません。
以上より、正解は 1 です。

コメント