問 題
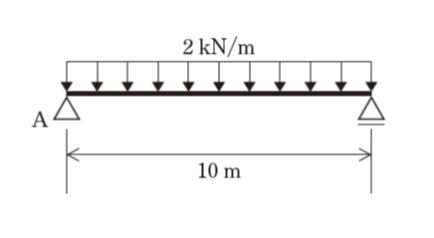
図のように、等分布荷重が作用し支点A に鉛直反力の生じた梁がある。この支点A の鉛直反力と大きさの等しい鉛直反力が支点B に生じた梁として最も妥当なのはどれか。ただし、梁の自重は無視できるものとする。
解 説
等分布荷重が作用している梁に注目します。
まず反力を求めます。反力を求める際は、等分布荷重は集中荷重に直します。
2kN/m が 10m なので、20kN の集中荷重がちょうど真ん中に作用します。対称性から、A の反力は 10kN と考えられます。
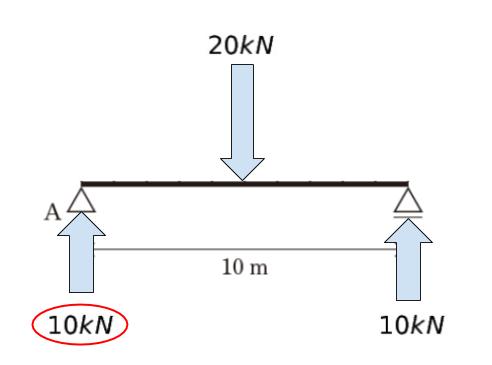
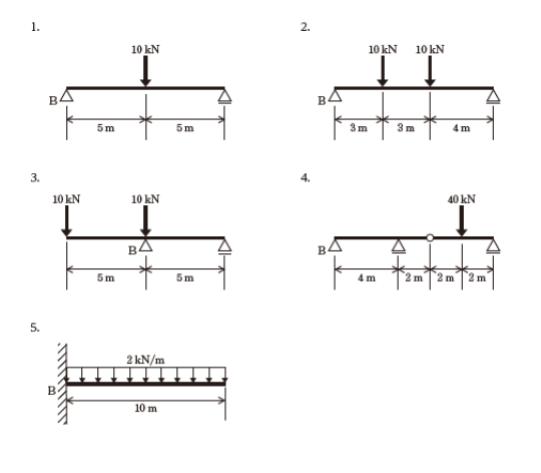
選択肢 1 ですが
明らかに 支点 B の反力は 5kN です。よって、選択肢 1 は誤りです。
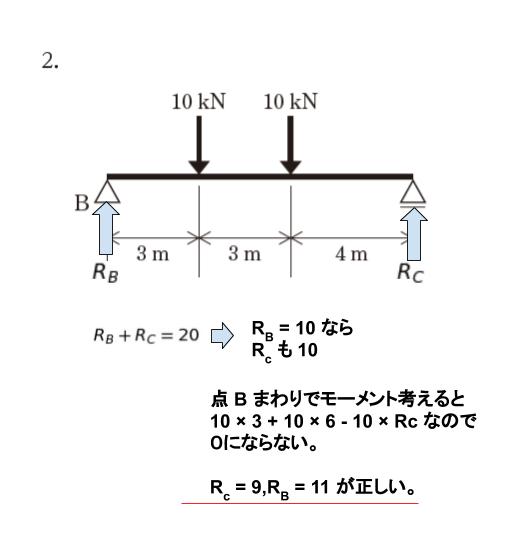
選択肢 2 ですが
B の逆のローラー部分の垂直反力を Rc とおきます。
縦の力の和が0なので、RB + Rc = 20 です。もしも RB = 10 とすれば、Rc も10 です。そうすると B 点まわりのモーメントを考えると 3× 10 + 6 × 10 – 100 ≠ 0 です。よって誤りです。
選択肢 3 ですが
B の逆のローラー部分の垂直反力を Rc とおきます。
縦の力の和が0なので、RB + Rc = 20 です。もしも RB = 10 とすれば、Rc も10 です。そうすると、A 点まわりのモーメントが 0 にならず誤りです。
選択肢 4 は妥当です。
ゲルバー梁と呼ばれる構造です。B から見て、ローラーを C,D とします。反力が 4 つになるのですが、ピン部分で切断して考えると反力を求めることができます。ピン部分はモーメントが0であることがポイントです。まず、ピンで切断した右側に注目すれば、ピンまわりのモーメントが 0 なので、RD = 20 が求まります。
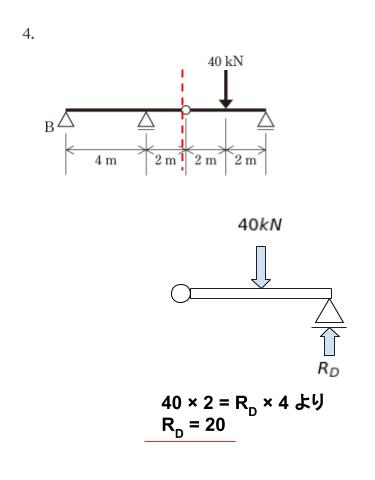
RD = 20 がわかったので、全体の縦の力の和に注目すれば、RB + Rc = 20 です。
そして、ピンで切断した左側に注目すれば ピン周りのモーメント 0 なので、Rc × 2 + RB × 6 = 0 です。式が2つなので、解けます。RB = -10 となり、大きさは確かに 10 です。
選択肢 5 の方が簡単なので、本番では 選択肢 4 をとばすことがおすすめです。
選択肢 5 の片持ち梁の等分部荷重を集中荷重になおせば 20kN です。B の鉛直反力は 20kN です。よって、選択肢 5 は誤りです。
以上より、正解は 4 です。

コメント