問 題
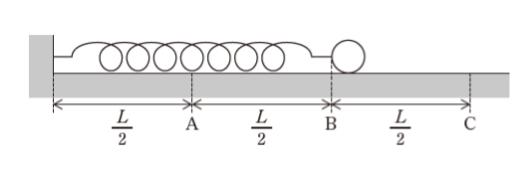
図のように、一端を壁に固定して滑らかな水平面上に置いた自然長 L のばねの他端に小球を取り付けた。壁から L/2 離れた点を A、L 離れた点を B、 3L/2 離れた点を C として、小球を点 C まで移動させ、静かに放した。
このとき、小球の運動エネルギーが最大となる点として妥当なもののみを全て挙げているのはどれか。
1.A
2.A、B、C
3.A、C
4.B
5.C
正解 (4)
解 説
水平ばね振り子において
弾性力による位置エネルギー U は、基準点(自然長)から x 離れた所において
U = kx2/2 です。これは知識です。
力学的エネルギー=位置エネルギー+運動エネルギー が成立します。ここで、運動エネルギー K = mv2/2 です。自然長が L なので問題文の図の状態において、位置エネルギーは 0 です。
C まで引っ張ることで、位置エネルギーが k(L/2)2/2、速度は 0 なので、運動エネルギーは 0 です。この和が力学的エネルギーです。力学的エネルギーは保存されます。手を離すと、位置エネルギーが 0 となる点、すなわち 点 B において、運動エネルギーが最大となります。
以上より、正解は 4 です。

コメント