H29年 国家一般職(高卒 技術) No.3 数学　解説

　問 題　　　　　

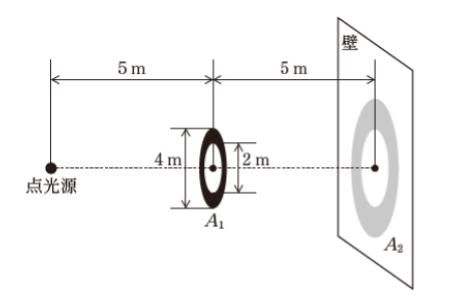
図のように、外径 4 m、内径 2 m で中空の薄い円板を、鉛直な壁と平行で、円板の中心と点光源を結ぶ直線が壁に垂直となるように固定したとき、壁に影が投影された。光が当たっている円板の面積 A1 と壁に投影された影の面積 A2 の比 A₂/A₁ はいくらか。

1. 1
2. 2
3. 4
4. 8
5. 16

 

 

 

 

 

　解 説　　　　　

A₁ は
「半径 2m の円の面積から、半径 1m の円の面積を引けば」求めることができます。

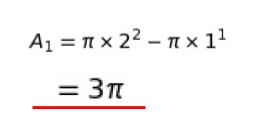
A₂ ですが
大きい方の円は、光が 5m 進むと外形の直径が 4m 大きくなっていると考えれば、壁に映る円の大きい方の直径は 8m です。同様に、小さい方の円の直径も、光が 5m 進むと 2m 大きくなっていると考えれば、壁に映る円の小さい方の直径は 4m です。

従って、A₂ は
半径 4m の円の面積から、半径 2m の円の面積を引けば求めることができます。

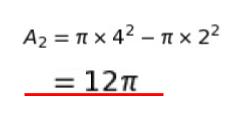
A₂/A₁ = 12π/3π = 4 です。

以上より、正解は 3 です。