公務員試験 H29年 国家一般職(土木) No.27解説

　問 題　　　　　

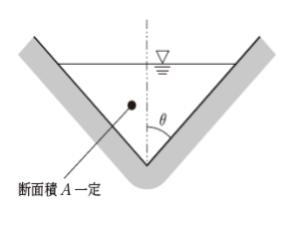
図のように、左右対称な三角形断面となる開水路に等流状態で水が流れているとき、次の記述の㋐、㋑、㋒に当てはまるものの組合せとして最も妥当なのはどれか。

ただし、0°＜θ＜90°であり、θによらず断面積Aは一定とする。

また、開水路の縦断勾配、水路床部の粗度係数は任意のθで等しいものとする。

「断面平均流速をvとしたとき、流量QはQ=Avで表され、vが最大となるθのとき、Qが最大となる。

vをマニングの平均流速公式で表せば、( ㋐ )が最小、( ㋑ )が最大となるθのときQが最大となる。

θ=30°のときの流量をQ_30°、θ=45°のときの流量をQ_45°とした場合、両者の大小関係は( ㋒ )となる。」

　　㋐　　　㋑　　　　　㋒

1．潤辺　　径深　　Q_30° ＜ Q_45°

2．潤辺　　径深　　Q_30° ＞ Q_45°

3．潤辺　　径深　　Q_30° =  Q_45°

4．径深　　潤辺　　Q_30° ＜ Q_45°

5．径深　　潤辺　　Q_30° ＞ Q_45°

 

 

 

 

 

　解 説　　　　　

マニングの式は絶対に正確に覚えておくべき公式です。

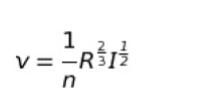
※ R は径深。A/S。Aは流積、Sは潤辺。

公式を見つつ選択肢を確認すれば、㋐は潤辺、㋑は径深です。

正解は 1~3 です。

θ = 30°,θ = 45°の時をそれぞれ考えてみると

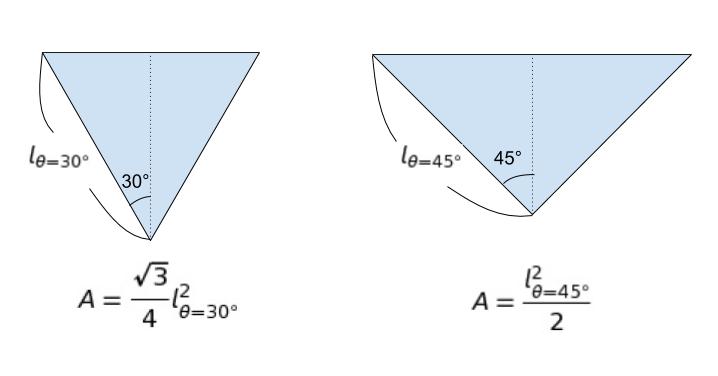
図のように表すことができます。潤辺は それぞれ l を 2倍したものです。つまり、l の大小がそのまま潤辺の大小となります。潤辺が大きい方が v は小さくなります。

A= ・・・の式を l² = ・・・になおしてみると、

θ = 30°の方は l² = 4/√3 A となります。

θ = 45°の方は l² = 2A となります。

√3 ≒ 1.7 なので、4/√3 > 2 です。従って、30°の方が l は大きいとわかります。

つまり、Qは 45°の方が大きいため、Q_30° ＜ Q_45°　です。

正解は 1 です。