問 題
図のように天井からつり下げられた長さ5aの棒に鉛直集中荷重Pが作用しているとき、次の記述の㋐~㋓に当てはまるものの組合せとして最も妥当なのはどれか。
ただし、棒の断面積をA、単位体積重量をw、ヤング係数をEとし、変形は軸方向のみ考えるものとする。
「棒の先端からxの距離にある点での応力σxは式①で表される。

また、応力σxによる微小要素dxの伸び量duとひずみεxの関係式は式②で表され、応力σxとひずみfxはフックの法則より式③で表される。
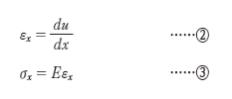
式②、式③より、微小要素の伸び量は式④で表される。

式①を式④に代入し、棒の全長にわたって積分すると、鉛直集中荷重による伸び量は( ㋒ )、自重による伸び量は( ㋓ )となる。」
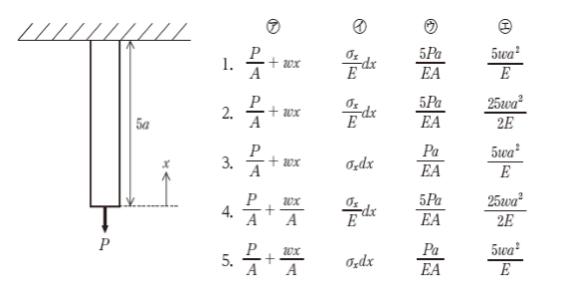
正解 (2)
解 説
x の距離までの体積が Ax です。単位体積重量が w とあるので、力は P+Axw かかっているはずです。
応力は「力/面積」なのでAで割れば、P/A + wx となります。正解は 1~3 です。
式②より、
du = εxdx です。
式③より
εx = σx/E です。 代入すれば
du = (σx/E)dx となります。
正解は 1 or 2 です。この時点で㋒は 5Pa/EA とわかります。
㋓の計算のために積分を問題文の指示に従って計算すると、以下のようになります。

従って、正解は 2 です。

コメント