公務員試験 H29年 国家一般職(土木) No.22解説

　問 題　　　　　

図のような三角形断面において、A軸、B軸、C軸に関する断面2次モーメントをそれぞれ I_A、I_B、I_C とするとき、これらの比として最も妥当なのはどれか。

ただし、A軸、B軸、C軸はそれぞれ底辺に平行であるものとする。

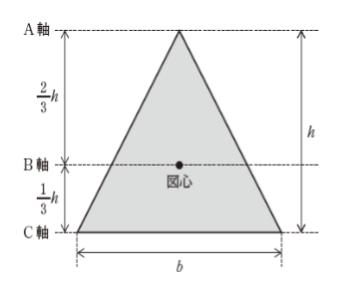
　I_A：I_B：I_C

1．5：1：3

2．5：2：3

3．5：3：2

4．9：1：3

5．9：2：5

 

 

 

 

 

　解 説　　　　　

図心を通る軸に関する三角形の断面二次モーメントは I = bh³/36 です。

また、図心を通らない場合の断面二次モーメントは「図心を通る場合の断面二次モーメント」＋Ay² です。

※Aは断面積です。
※y は軸から図心までの距離です。

以上が基礎知識となります。

本問では、A = bh/2 です。従って、I_A、I_B、I_C はそれぞれ

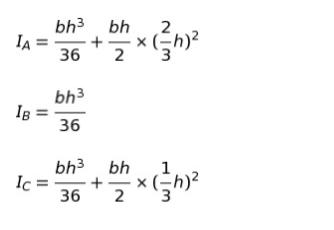
と表すことができます。定数係数部分のみに注目すれば、9/36：1/36：3/36 となります。

36 倍すれば、9：1：3 です。

正解は 4 です。