問 題
y=x2、x=1及びx軸で囲まれたxy平面上の領域を、y軸のまわりに1回転してできる立体の体積として正しいのはどれか。
正解 (5)
解 説
【解法1 体積の大雑把な評価】
下図のように考えれば、求める体積は半径 1,高さ 1 の円錐よりも少し大きい体積と評価できます。
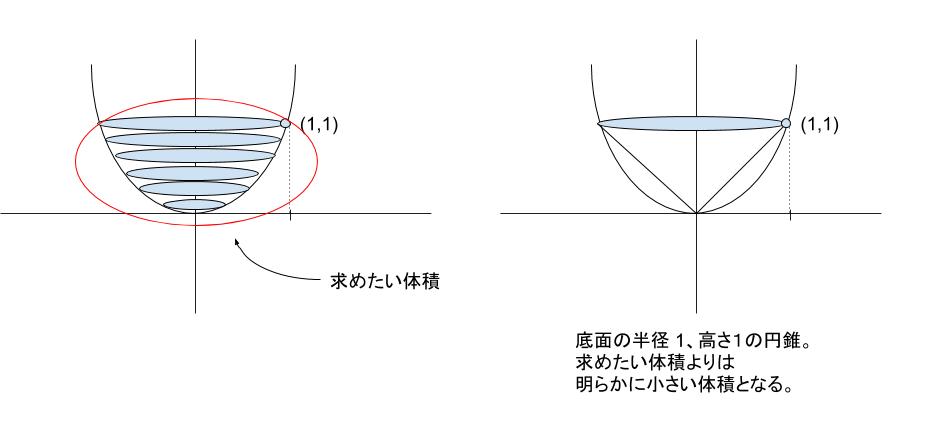
半径 1 、高さ 1 の円錐の体積は
V = π × 1 × 1/3
= π/3 です。
選択肢の中でこれより大きいのは、π/2 です。
正解は 5 です。
【解法2 積分計算】
「y軸周りの回転」なので ∫ πx2 dy を計算します。
y = x2 なので、x2 = y です。また、積分範囲は y = 0 ~ y=1 です。
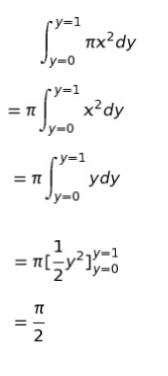
以上より、正解は 5 です。

コメント