問 題
xy平面上の点(1、-1)から曲線 y = 1/3 x3 ー x に傾きが正の接線を引いたとき、その傾きの値として正しいのはどれか。
- 1/2
- 3/4
- 5/4
- 3/2
- 7/4
解 説
【解法1 大雑把な評価で選択肢を絞る】
y = 1/3 x3 ー x のグラフをできるだけ正確に書きます。x = 0 の時、y = 0 です。また、右辺は
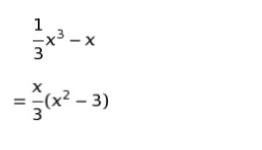
とかけるので、x = ±√3 の時も y = 0 です。以上を参考にして、下図のようになります。
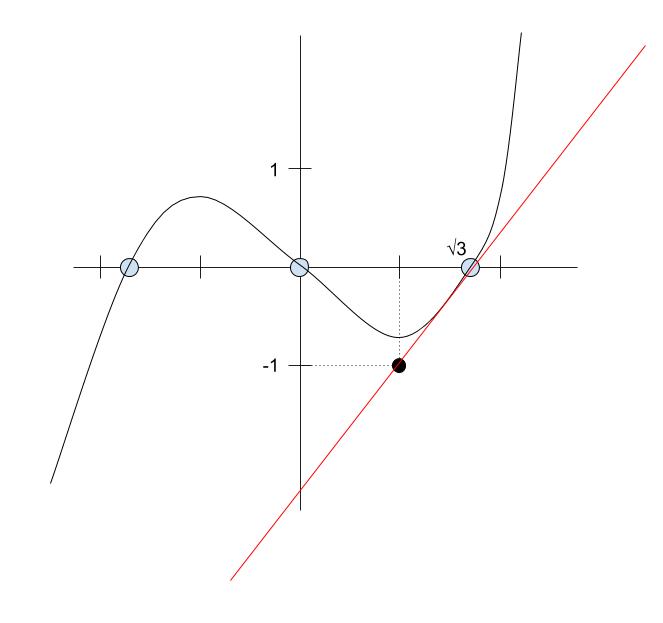
赤い線が接線です。すると、接線の傾きは「(1,-1)と(√3,0)」を結ぶ直線よりも少し小さい傾きである と評価できます。√3 ≒ 1.7 です。
従って、「(1,-1)と(√3,0)」を結ぶ直線 は右に 0.7 進んで、上に 1 上がる直線です。この傾きは、1/0.7≒ 1.4 です。
これより少し小さい傾きとなれば、選択肢の中では 5/4 となります。
よって正解は 3 です。
【解法2 微分で求める】
y = 1/3 x3 ー x を微分すると、y’ = x2 ー 1 です。
接点を(t,1/3 t3 ー t)とおきます。接線の傾きは (t2 ー 1) とかけます。
接線の式は
l:y = (t2 ー 1) x +β
とおくことができ、点(t,1/3 t3 ー t)を通ることから、
β = ー2/3 t3
とわかります。
改めて、接線の式は
l:y = (t2 ー 1) x +(ー2/3 t3)
です。点(1,-1)を通る時、
-1=(t2 ー 1) ー2/3 t3
が成り立ちます。
ー2/3 t3 + t2 = 0
ー2/3 t + 1 = 0
∴ t = 3/2 です。
※ここで正解が 4 と間違えないように!
※この t は接点の x 座標です。傾きではありません。
接線の傾きは
(3/2)2 ー1
= 9/4 ー1
= 5/4 です。
正解は 3 です。

コメント