公務員試験 H29年 国家一般職(土木) No.1解説

　問 題　　　　　

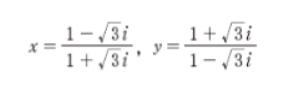
のとき、x³ + y³ の値はいくらか。ただし、i は虚数単位とする。

1．－56

2．－28

3．－2

4．2

5．28

 

 

 

 

 

　解 説　　　　　

解法１【絶対値,偏角を考える】

ある 2つの複素数Z₁,Z₂の商において、それぞれの絶対値を r₁,r₂、偏角を θ₁,θ₂ とおけば、Z₁/Z₂ の絶対値は r₁/r₂ です。Z₁/Z₂ の偏角は θ₁ーθ₂ です。

下図のように複素平面を考えれば、「1＋√3i」,「1ー√3i」 は、絶対値は共に２、偏角はそれぞれ 60°,ー60°です。

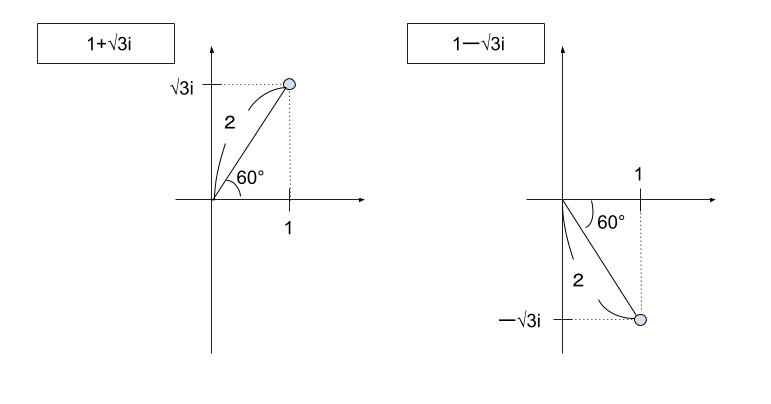
x は「1ー√3i」/「1＋√3i」 です。よって、x の絶対値は1,偏角は ー120°です。

y は「1＋√3i」/「1ー√3i」です。よって、y の絶対値は1,偏角は 120°です。

複素数において　n乗すると絶対値は n 乗されて、偏角は n 倍されます。従って、

x³ の絶対値は1,偏角は ー360°です。

y³ の絶対値は1,偏角は 360°です。

結局、x³ も、y³ も１とわかります。従って、x³+y³ = 2 です。

正解は 4 です。

---

解法２【対称式なので、基本対称式 x+y,xy で考える】

※対称式　とは、文字を入れ替えても同じ式になる式。

x+y = -1
xy = 1 となります。

計算は以下のようになります。

xy については、約分で１です。

x³ + y³
= (x+y)³ -3xy(x+y) です。

※これは対称式の変形に関する基本知識。

以上より

x³ + y³
= (ー1)³ー3×1×(－1)
= 2 です。

正解は 4 です。