公務員試験 H29年 国家一般職(電気・電子・情報) No.37解説

　問 題　　　　　

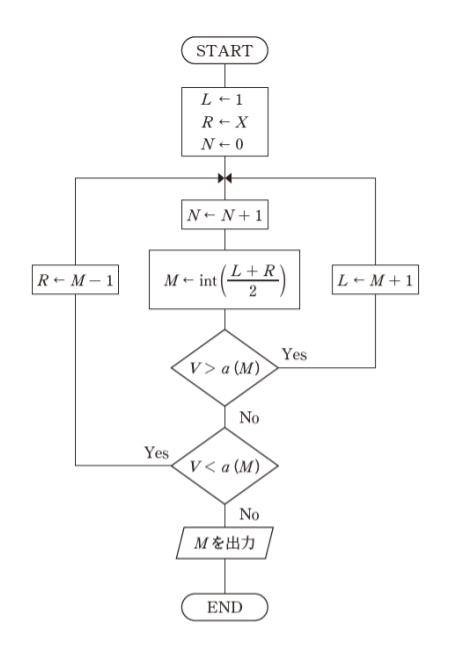
図は, X 個の異なる要素が昇順に並べられた配列a から, 配列に含まれる指定値V を2 分探索法によって探索するためのフローチャートである。

512 個の異なる要素が昇順に並べられた配列について,  2 分探索法により配列中の値を検索するとき, 図中のN がとり得る最大の値はいくらか。ただし, int （）は引数の小数点以下を切り捨てて整数を返す関数であり, a（M）は配列 a の M 番目の要素である。

1. 6
2. 8
3. 10
4. 12
5. 14

 

 

 

 

 

　解 説　　　　　

512 = 2⁹ です。いきなりこれはわかりにくいので、具体的かつ簡単なデータ数 1 = 2⁰、2 = 2¹ の場合をそれぞれ考えてみます。

データ数 1 であれば、チャートをまっすぐ読んでいくことになり、 N = 1 です。

データ数 2 で、データの中身が 1,2 で、探索しているのが 2 とします。すると、チャートを読んでいけば
『
(L,R,N,M)=(1,2,1,1)y
(L,R,N,M)=(2,2,2,2)nn で END となり、N = 2 です。
』

傾向として、データ数 2ⁿ の場合、最悪 n+1 が N のとり得る最大値と見られます。よって、データ数 2⁹ であれば、最悪の N は 10 です。

以上より、正解は 3 です。