公務員試験 H29年 国家一般職(電気・電子・情報) No.23解説

　問 題　　　　　

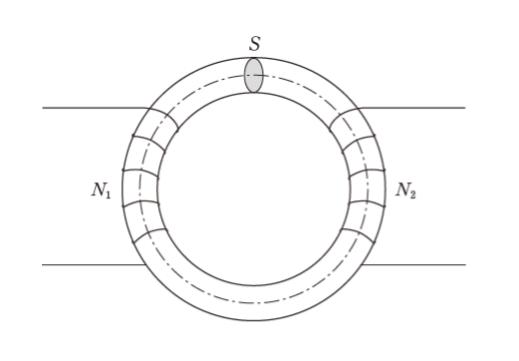
図のような断面積が S の環状磁性体に巻かれた二つのコイルがある。それぞれのコイルの巻数を N1 と N2 とするとき，両者の間の相互インダクタンス M に関する記述として最も妥当なのはどれか。ただし，磁束は磁性体の外部に漏れないものとする。

1．N₁ のみを 2 倍にしたとき，M は 4 倍になる。
2．N₁ のみを 4 倍にしたとき，M は 2 倍になる。
3．N₁ を 2 倍，N₂ を 2 倍にしたとき，M は 4 倍になる。
4．S を 2 倍にしたとき，M は 4 倍になる。
5．S を 4 倍にしたとき，M は 2 倍になる。

 

 

 

 

 

　解 説　　　　　

インダクタンスを考える時は「ある回路に電流流れる→磁界発生→回路をどれだけ磁束が貫くかを考える」という流れが基本です。そして、環状磁性体内部であれば、磁束が漏れないから、貫く磁束が一定ということで計算が簡単になります。また、２つの回路間の相互インダクタンスについては、どちらか一方に電流を流して計算できる相互インダクタンスを計算すれば OK です。

左側をコイル１と名付け、電流 I を流す場合を考えます。アンペールの積分法則より、環状磁性体内部を一周する長さを l とおけば Bl = μN₁Ｉです。よって磁束密度 B は μN₁Ｉ/ l です。まずこれが磁束「密度」です。断面積 S だから、BS が磁束です。そして『コイル C1 を貫く全磁束』は N₁ × BS となります。

従って
『コイル１に流れる電流により生じる磁束により、コイル１が貫かれる全磁束』 を Φ₁₁ とおけば、 Φ₁₁ = N₁ × BS = N₁ × μN₁ＩS/ l と表せます。Ｉの係数が「自己インダクタンス」です。自己インダクタンスは μN₁²S/l と表すことができます。

次に
コイル１に流れる電流により生じる磁束により、コイル C₂ を貫く全磁束は N₂BS なので、N₂ × μN₁ＩS/ l です。やはりこのＩの係数に注目すれば、この係数が「相互インダクタンス」です。つまり μN₁N₂S/l が相互インダクタンスです。すると、相互インダクタンスは N₁,N₂ に比例するとわかります。また、S とも比例します。

以上より、正解は 3 です。
類題 H25no23