問 題
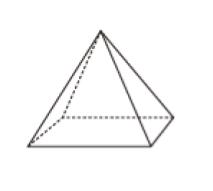
紙粘土を用い,各辺の長さが 70 cm である中身の詰まった底面が正方形の四角錐を作ることとした。
そのもととなる紙粘土の塊が、1 個 700 cm3 であるとき,この四角錐を作るために必要な紙粘土の塊は最低で何個か。
ただし, √2 = 1.41 とする。また,紙粘土は,変形させても,体積が変わらないものとする。
1. 106 個
2. 116 個
3. 126 個
4. 136 個
5. 146 個
正解 (2)
解 説
正四角錐の体積は 、一辺を a とすると V = √2 a 3 /6 です。公式として覚えておくとよいです。 a = 70 なので、70 × 70 × 70 = 70 × (10 × 7) × 70 = 700 × 490 とすることで、紙粘土何個分か考えやすくなります。
体積が 700 × (√2/6 ) × 490 と表せるため、 (√2/6 ) × 490 が選択肢のうちどれか、という問題です。 √2 = 1.41 とすると、うまく約分できて (√2/6 ) × 490 = 0.47 × 245 となります。計算すると 115.15 なので、ほぼ 116 です。
よって、正解は 2 です。

コメント