問 題
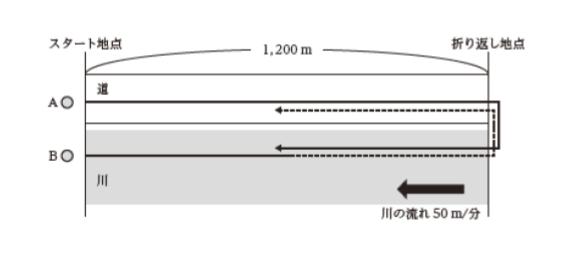
AとBは,図のように分速50 m で真っすぐに流れている川と,この川に平行している片道1,200 m の道をそれぞれボートと自転車を使って往復した。
Aは自転車に乗って分速300 m でスタート地点を出発し,折り返し地点からボートに乗ってスタート地点まで川を下流に向かって戻った。一方,Bはボートに乗ってスタート地点から川を上流に向かって出発し,折り返し地点から6 分間自転車に乗ってスタート地点まで戻った。
また,AとBが,それぞれスタート地点に戻ってくるまでの所要時間の差は18 分であった。
さらに,AとBが乗ったボートの速さは,川の流れがない場合に同じであった。このとき,川の流れがない場合のボートの速さはいくらか。
ただし,ボートや自転車の速さは,AとBのそれぞれで一定であるものとし,ボートや自転車の乗換えに要する時間はなかったものとする。
1.分速75 m
2.分速100 m
3.分速125 m
4.分速150 m
5.分速175 m
解 説
いわゆる流水算です。流れの速さ分足したり引いたりしなければならない点に注意します。選択肢の中できれいな値から試してみます。川の流れがない場合のボートの速さを 100m/分とします。
A は、まず自転車 300m/分 で 1200m 行くので、4 分で折り返し地点につきます。ボートに乗り、流れ方向に進むので 、速さは (100+ 50) m/分 です。よって、8 分で スタート地点に戻ってきます。合わせて 4 + 8 = 12 分です。
一方、B は、ボートで出発しています。流れと逆方向なので、速さは(100 ー 50)m/分です。よって、24 分で折り返し地点につきます。そして 6 分でスタート地点まで戻るので、合わせて 24+6 = 30 分です。差がちょうど 18 分なので、これが正解です。
以上より、正解は 2 です。

コメント