問 題
質量 m の気体分子が温度 T の下にあるとき、速さ v の分子の割合は、ボルツマン定数を k として
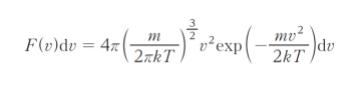
で示されるマクスウェル-ボルツマン分布に従う。ここで、F(v) は速さの分布関数といい
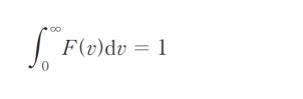
である。
また、気体分子の速さについては、平均速さ 及び 根平均 2 乗速さ それぞれ
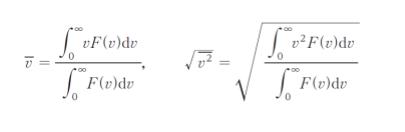
で表される。
平均速さ 及び 根平均 2 乗速さを、T 及び気体のモル質量 M 、気体定数 R で表したものの組合せとして最も妥当なのはどれか。なお、必要であれば
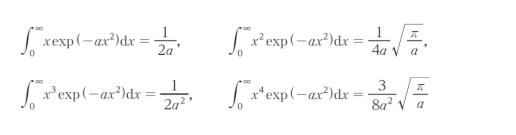
を用いてよい。

解 説
選択肢を見ると、大体同じような式になっており、左側の √の 中身の何倍かが右側の式になっています。
詳しく見ると
選択肢 1 は × 3/2
選択肢 2 は × 2π/8
選択肢 3 は × 3π/8
選択肢 4 は × 2/3
選択肢 5 は × 8/3π です。
知識として、根平均二乗速さが一番大きくなることを覚えていれば、π ≒ 3 と近似して考えると、この時点で正解は 1 or 3 です。∵選択肢 2,4,5 では根平均二乗速さの方が小さくなってしまう。
選択肢 1 と 3 のどちらが正解かを考えるためには、π の次数にだけ注目すれば十分です。vF(v) を考えると、v の次数が 3 となるので、公式の 左下が使えると考えられます。同様に、v2F(V) を考えれば、v の次数が 4 となるので、公式の右下を使うことになります。すると、公式の右辺に注目すると π の次数が ½ 増えるとわかります。これで、正解は 3 と選ぶことが出来ます。
ーーーーーー
ーーーーーー
全く知識がなかった場合も、なんとか与えられた情報を活用していくことで、時間がかかっても答えを選びたい問題です。
まず公式と F(v)dv を比較することで、「a」 = 「m/2kT」,「x」 = 「v」 と設定します。さらに温度 T も定数であることに注意します。また、平均速さ、及び、根平均 2 乗速さ の式において「分母は結局 1」 なので気にする必要はなく、略してOKです。
選択肢に注目すれば、結局 π の次数と定数部分だけ注目すればよいと考えて式に注目します。「vF(v)dv」 に関して、公式使えそうな部分が、x3exp(-ax2) です。この部分が 1/2a2 になるということです。一方、v2F(v)dv になると、公式使えそうな部分が、x4exp(-ax2)=3/8a2 ×√π/a です。a の中身において定数部分は、1/2 です。
以上をふまえ、まず平均速さの定数部分のみを計算してみます。

平均速さの定数部分については、√8 となります。
同様に根平均 2 乗速さの定数部分を計算すると

となり、√3です。
以上より、正解は 3 です。

コメント