問 題
ある国のマクロ経済が,以下の式で示されているとする。

いま,この経済において,政府支出を 60 % 拡大した。この場合におけるクラウディング・アウト効果による国民所得の減少分はいくらか。
1. 8
2. 12
3. 16
4. 20
5. 24
解 説
「財政政策→利子率増加→投資減少」という流れが「クラウディングアウト」です。政府による公共投資や減税といった財政政策は、IS 曲線を右にシフトします。結果、国民所得 Y は増加します。
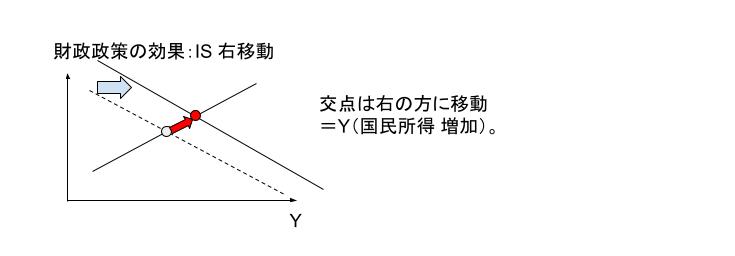
クラウディングアウト効果による減少分とは、財政政策を行い、「利子率が変わらなかった場合の均衡点における国民所得」と比較した時の差分です。下図における赤両矢印部分です。
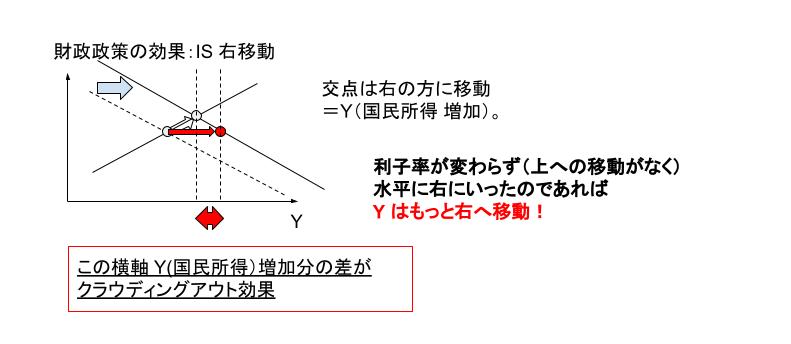
まず、与えられた式から、IS 曲線 及び LM 曲線を求めます。上 6 つの生産物市場(=財市場)に関する式にまず注目します。一番上の式に、2番目、3番目・・・の式を代入し、r = … という形に整理します。この式が表すのが IS 曲線となります。
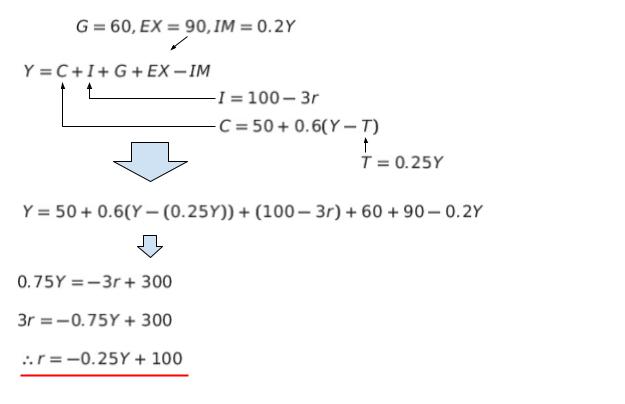
次に、残りの貨幣市場に関する式に注目します。M/P = L が貨幣市場の均衡式です。この均衡式は基礎知識として知っている前提です。本問では M=L なので、P=1 と考えられます。代入していけば 100 = Y – 8r + 60 なので、r について解けば、r = Y/8 -5 です。これが LM 曲線です。
2つの直線の交点を、連立方程式を解くことで求めると、(Y,r) = (280,30) です。
【政府支出が 60% 拡大】
次に、政府支出が 60% 拡大した場合を考えます。政府支出 G = 60 が 60% 拡大すると、G’ = 96 です。これを代入して、改めて計算すると IS 曲線は 3r = -0.75Y + 336 → r = -0.25Y + 112 となり、右に移動します。 この新しい IS 曲線と、r = Y/8 – 5 の交点を改めて、連立方程式を解くことで求めると、(Y,r) = (312,34) です。
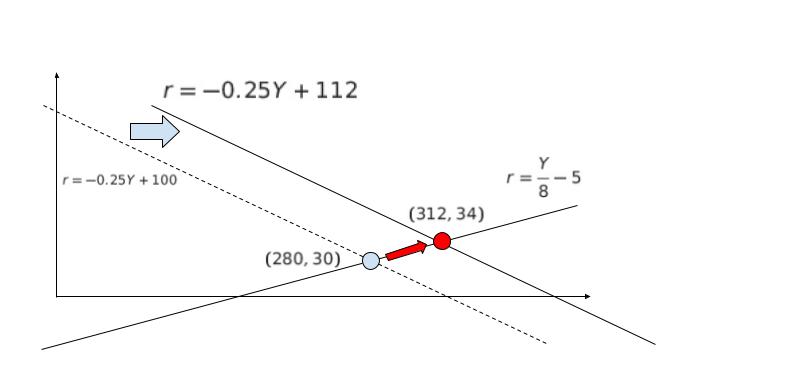
一方、利子率が変わらなかったら、と仮定します。r = 30 を新しくできた IS 曲線の式:r = -0.25Y + 112 に代入して Y を求めると、Y = 328 です。従って、クラウディングアウト効果による減少分は、328 ー 312 = 16 です。
以上より、正解は 3 です。

コメント