H28年 国家一般職(高卒 技術) No.4 数学　解説

　問 題　　　　　

sin π/4、sin 3π/4、sin 5π/4、sin 7π/4 の大小関係として正しいのはどれか。

1.sin π/4 = sin 3π/4 < sin 5π/4 = sin 7π/4
2.sin π/4 = sin 7π/4 < sin 3π/4 = sin 5π/4
3.sin 3π/4 = sin 5π/4 < sin π/4 = sin 7π/4
4.sin 3π/4 = sin 7π/4 < sin π/4 = sin 5π/4
5.sin 5π/4 = sin 7π/4 < sin π/4 = sin 3π/4

 

 

 

 

 

　解 説　　　　　

π = 180° です。180°を越える三角関数なので、単位円の定義を思い出します。単位円（半径 1 の円）を考えて、原点から θ 方向にビームを放ち、単位円との交点の x 座標、y 座標をそれぞれ x,y とします。この x 座標が cos θ、y 座標が sin θ です。ちなみにこの時、tan θ = y/x です。

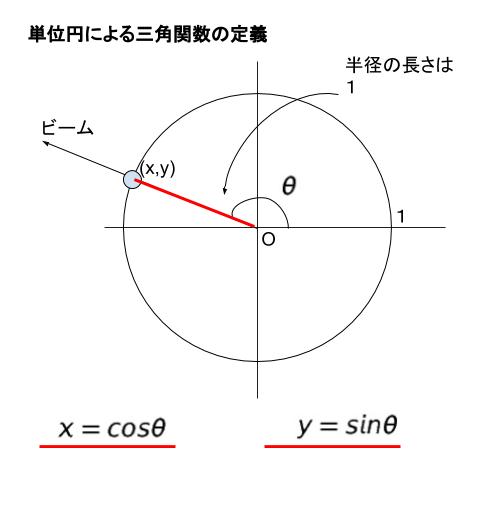
すると、sin π/4 (sin45°) と sin 3π/4 (sin135°) は、交点の y 座標が同じになります。

同様に考えれば、sin 5π/4 = sin 7π/4 です。そして、sinπ/4 の方が、値は正なので大きいです。
「sin 5π/4 = sin 7π/4 < sin π/4 = sin 3π/4」が正しいとわかります。

以上より、正解は 5 です。