問 題

図のように,直角三角形 ABC の内接円 O と辺 AB,BC,CA の接点をそれぞれ P,Q,R とする。AR = 2,BP = 3 のとき,辺 BC の長さはいくらか。
1. 10
2. 11
3. 12
4. 13
5. 14
正解 (4)
解 説
AP = 2、BQ = 3 がすぐ読み取れるかどうかがポイントです。
「円外の一点から引いた2つの接線を考えた時、接点までの距離は等しい」が図形の基礎知識です。
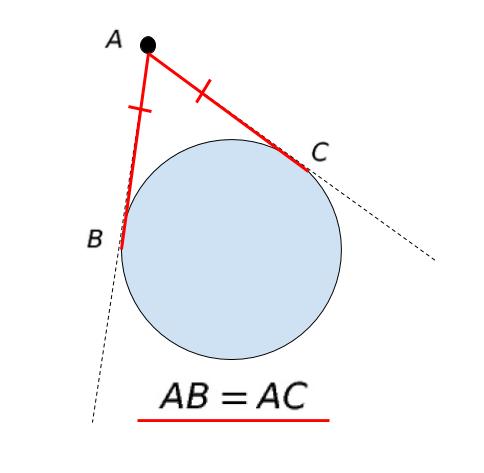
CR = x とおくと、CQ = x です。求めたい BC = BQ + QC = 3 + x です。
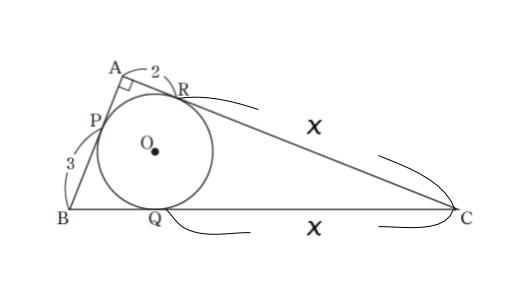
選択肢より、BC の候補が 10,11,12,13,14, なので、CQ の候補は 7,8,9,10,11 です。
代入して考えてみると、x = 10 の時、直角三角形 ABC の辺の比が 5:12:13 と、有名頻出の辺の比になるため、これが正解と考えられます。
以上より、正解は 4 です。
※ BC の長さなので、1 ではない点に注意です!

コメント