問 題
2 次方程式 x2 – 4x + 2m = 0 が異なる二つの実数解をもつような定数 m の値の範囲として正しいのはどれか。
1.m > -4
2.m > -2
3.m < 2
4.m < 4
5.m < 8
正解 (3)
解 説
「異なる 2 つの解を持つ」とは、y = x2 – 4x + 2m ・・・ (1) のグラフと y = 0 のグラフの交点が 2 つあるということです。 y = 0 とは x 軸に他なりません。すると、(1) のグラフの頂点の y 座標が負であれば、交点2つとなります。
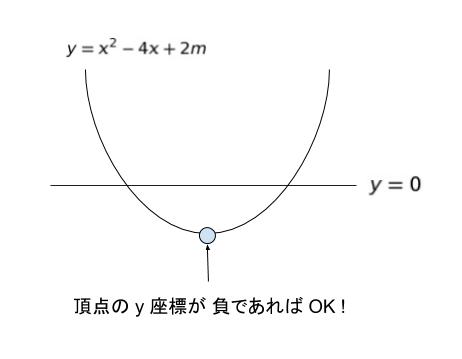
頂点の軸は y = ax2 + bx + c において、x = ーb/2a です。これは基礎知識です。平方完成をしてもOKです。
y = x2 -4x + 2m の頂点の x 座標は、軸の公式より ー(-4/2) = 2 です。これは y = (x-2)2 -4 + 2m と変形して見つけてもかまいません。
x = 2 を代入してみると y = 4 ー 8 + 2m = -4 + 2m です。
-4 + 2m < 0 であれば、交点2つです。従って、2m < 4 ∴m < 2 です。
以上より、正解は 3 です。

コメント