問 題
x>0、y>0、x+y=1のとき、log2x+log2yの最大値はいくらか。
- -2
- -1
- 0
- 1
- 2
解 説
【解法1:対数方程式として考える】
対数方程式の最大・最小問題としてとらえると、文字が2つなので x + y = 1 ↔ y = 1 – x を利用して1文字にします。
log2x + log2(1-x)
= log2x(1-x) です。
ここでg(x) = x(1-x) とおけば、g’(x) = -2x+1 です。よって、x = 1/2 の時 g’(x)= 0、この時が 最大と考えられます。
x = 1/2 の時、y = 1/2 です。log2x+log2y の値は -2となります。
従って正解は 1 です。
以下は解法1がしっくり来ない人やあっさりと解ける人用。色々な解き方を通じて、選択肢を消すことができるツールを一つでも多く身につけてみてください!
【解法2 具体的に(色々)考える】
x>0、y>0、x+y=1 なので、x も y も 0~1 の範囲です。y = log2x のグラフの概形を思い出せば、x の所に 0~1 までしか入らないのであれば log2x の値は明らかに負です。
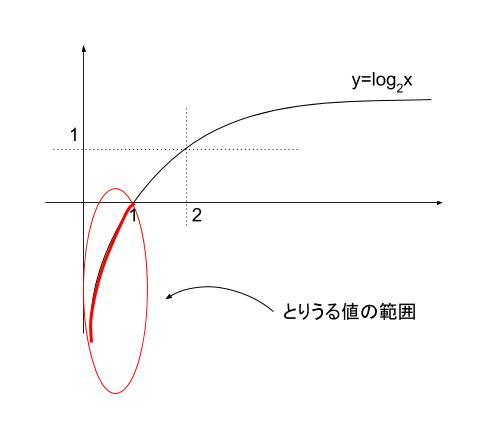
log2x+log2y はどちらの項も絶対に負なので、正解は 1 or 2 となります。
ぜひここまでは確実に選択肢をしぼってほしい問題です。
次に、「log2x+log2y = -1」 がなりたつかを検討します。成り立つ x,y があれば正解は 2 です。なければ正解は 1 となります。
log2x + log2y = log2xy と表せます。従って、log2x + log2y = -1 がなりたつならlog2xy = -1 です。つまり xy = 1/2 です。
x>0、y>0、x+y = 1 かつ xy = 1/2 が成り立つような x,y の組があるか を考えます。
2-1【それぞれのグラフで考える】(個人的にはこれが一番わかりやすくて好きです。)
xy = 定数 という式は反比例のグラフです。xy = 1/2 では (1,1/2),(1/2,1) を通るのが明らかなので、以下のようなグラフになります。
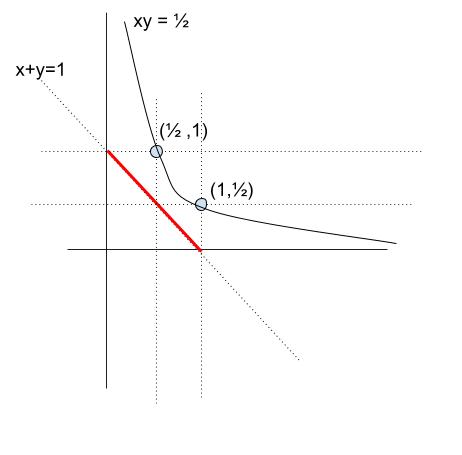
明らかに 2 つのグラフは交わりません。つまり、2つの式を同時に満たす x,y の組はありません。よって、正解は 1 です。
2-2【解と係数の関係で考える】
解と係数の関係より x+y = 1,xy = 1/2 を満たす x,y とは
「x2 – x + 1/2 = 0」・・・(1)
を満たす2つの解 x1,x2 に他なりません。
(1)の判別式を考えると、D = 1 -2 = -1 < 0 なので、この式(1)は実数解を持ちません。
よって、正解は 1 です。
2-3【相加相乗で考える】
1/2 (x+y) ≧ √xy なので、√xy ≦ 1/2、xy ≦ 1/4 となります。従って、xy = 1/2 は無理です。
よって、正解は 1 です。

コメント