問 題
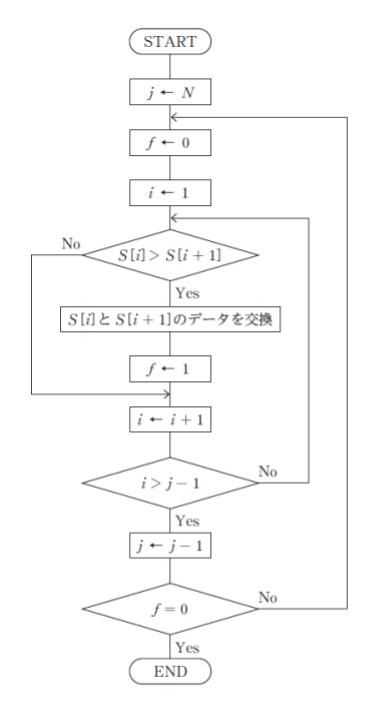
互いに値が異なる N(N>1) 個の整数が配列 S の 1 番目から N 番目の要素にあらかじめ格納されている。この配列を図のアルゴリズムを用いて並び替えた。データを交換する回数が最大となる場合の交換回数として最も妥当なのはどれか。
1. N 回
2. 2N- 1 回
3. N2 回
4. N(N-1) 回
5. N(N-1)/2 回
正解 (5)
解 説
このアルゴリズムは、隣接するデータを比較し「左の方が大きい」場合に2枚を交換する というのを順序よく行っています。(いわゆるバブルソートです。)その最悪を考えるので、一例として N=3 として、3,2,1 という順番に格納されているとします。
すると、まず「3を右端」に持っていくために「2回(3↔2、3↔1)」の交換が必要です。次に2を右端に持っていくために 「1回(2↔1)」の交換が必要です。これが最悪のパターンと考えられます。すると N個あった時に、逆順に並んでいると最悪で、その際必要な交換回数は「(N-1)+(N-2)+・・・+2+1」→N(Nー1)/2 が最悪と考えられます。
この計算ができなくても、N = 3 の時3になるのは選択肢から 1 or 5です。次に、N = 4 の時 6回 になるものを考えれば、 N(Nー1)/2 とわかります。
以上より、正解は 5 です。

コメント