問 題
4人でじゃんけんを1回行うとき、2人だけが勝つ確率及び、あいこになる確率の組合せとして正しいのはどれか。ただし、4人はグー、チョキ、パーをそれぞれ1/3の確率で出すものとする。

解 説
【解法1 数え上げる】
以降、4人を A,B,C,D と呼びます。A がグー、チョキ、パーのどれを出そうが確率は変わらないはずです。そこで、Aがグーと固定して考えます。
残りの B,C,D がそれぞれ3種類出す手があるので、33 = 27 通りについて考えます。以下の表のようにまとめることができます。
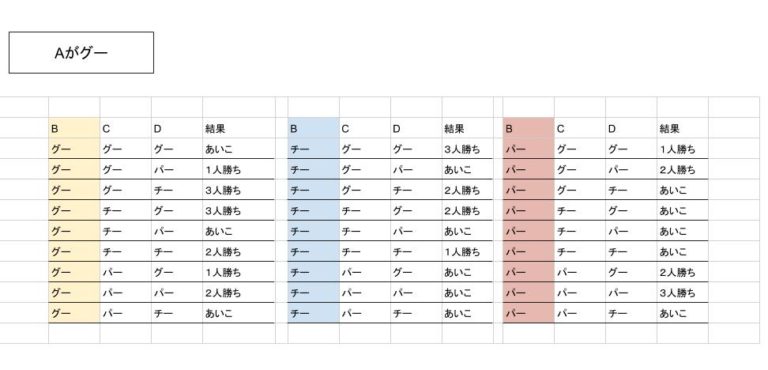
2 人だけ勝つ確率は、6/27 です。あいこの確率は 13/27 です。
以上より、正解は 4 です。
【解法2(確率が好きだったり、いつもかけぐるってる人用)】
『2人だけ勝つ確率について』
勝つ2人の選び方は、「A,B、A,C、A,D、B,C、B,D、C,D」 と6通り考えられます。グーで勝つ、チョキで勝つ、パーで勝つ という3通りがあるので
6×3/81
=18/81
=6/27 です。正解は 4 or 5 です。
『あいこの確率について』
あいこの確率はスパッとはわかりません。そこで、じゃんけんのパターンを、場に出た手の種類で分けると以下の3種類となります。
1:4人とも3種類のうち1種類しか出さない
=あいこ
2:4人とも3種類のうち2種類しか出さない
=誰かが勝つ
3:3種類全てが手として出る
=あいこ です。
あいこになる、簡単な場合としてパターン1から考えます。
【パターン1 1種類のみ】
ある一種類として、グー、チョキ、パーの3つがあります。それぞれの場合について
(1/3)4 = 1/81 の確率です。従って、パターン1が成立する確率は、1/81 × 3 = 3/81 です。
パターン 3 は複雑なので、パターン 2 の確率を計算し、余事象として考えることによりパターン 3 の確率を求めます。
【パターン2 2種類のみ】
2種類の選び方は、3つあります。すなわち「グーとチョキ のみ」、「グーとパー のみ」、「チョキとパー のみ」 の3つです。それぞれの場合について、(2/3)4 で成立しそうですが、これでは「全員がグー」のような『1種類のみの場合』を含んだ確率となっていることに注意が必要です。
・全員がグー→(1/3)4
・全員がチョキ→(1/3)4 といった形で「2×(1/3)4」を引きます。
よって、それぞれの場合について、(2/3)4 ー2×(1/3)4 =14/81 の確率です。従って、パターン 2 が成立する確率は、14/81 × 3 = 42/81 です。パターン1と2を合わせると 45/81 なので、パターン3の確率は、1- 45/81 = 36/81 です。あいこの確率は、パターン1とパターン3なので、39/81 =13/27 です。
以上より、正解は 4 です。

コメント