問 題
同じ大きさの立方体 27 個を隙間なく積み重ねて右のような大きな立方体を作った。
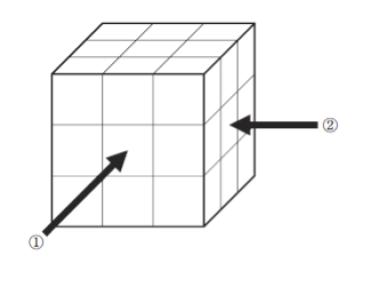
これから小さな立方体をいくつか取り除いてできた立体を ① 及び ② の矢印の方向から見たところそれぞれ図Ⅰ及び図のようになった。
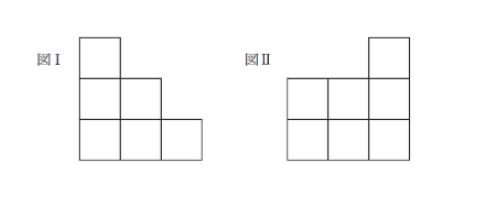
このとき残った立方体の個数として考えられる最小の個数はいくらか。ただし上部の立方体が取り除かれない限り,その真下に位置する立方体を取り除くことはできないものとする。
- 8個
- 10個
- 13個
- 16個
- 18個
正解 (1)
解 説
H26 no21 をふまえ、一段ずつ考えるとやりやすいです。
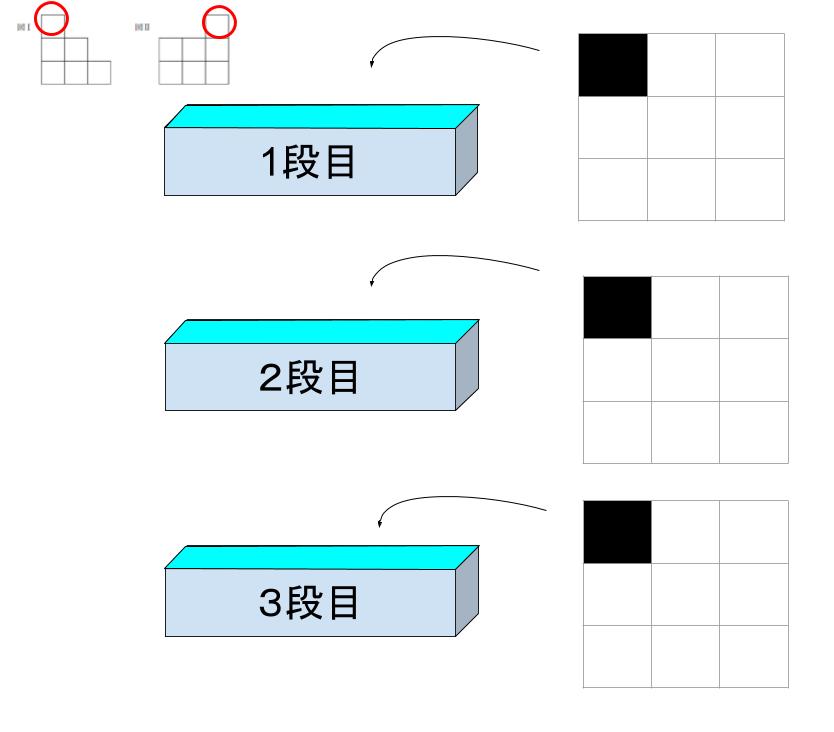
図Ⅰ、及び Ⅱ における、一番上の段の見た目を満たすためには、1段目の左上があればOKです。一番上に立方体を乗せるために、2 段目、3段目も左上は必要です。一例として、以下の図のようにまとめることができます。
次に2段目について、図Ⅰの2段目右側がすかっと抜けているので、2段目の右列は全て取り除かれていなければなりません。最小限残すと、2段目に立方体を置くためには、3段目の同じマス目にも必要な点に注意すると、一例として以下のようにすればよいとわかります。
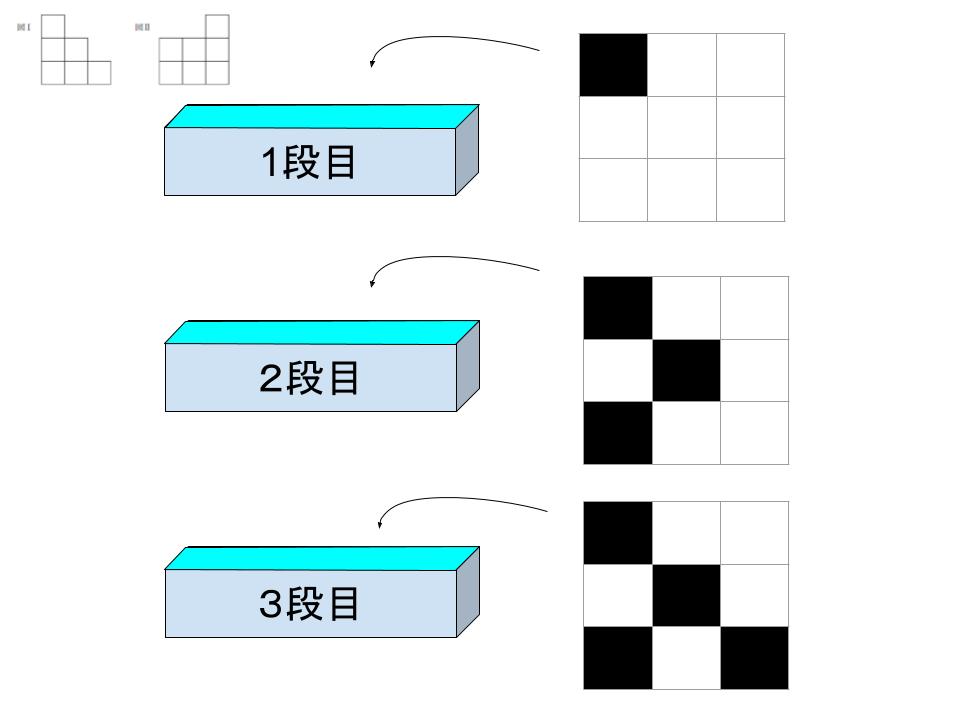
よって最小の個数は 8 個です。正解は 1 です。

コメント