問 題
図のように点B を中心に半径 √2 の扇形を反時計回りに30°回転させたとき、弧AB の通過する斜線部の領域の面積はいくらか。
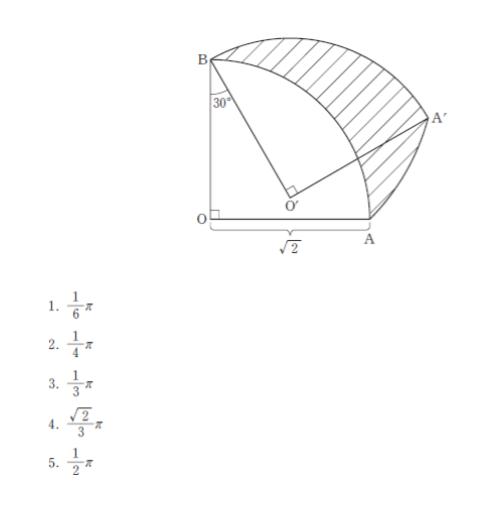
正解 (3)
解 説
BA,BA’ に補助線を引いて、同じ面積の部分を移動することで、結局扇形 BAA’ の面積を考えればよいとわかります。(下図参照)
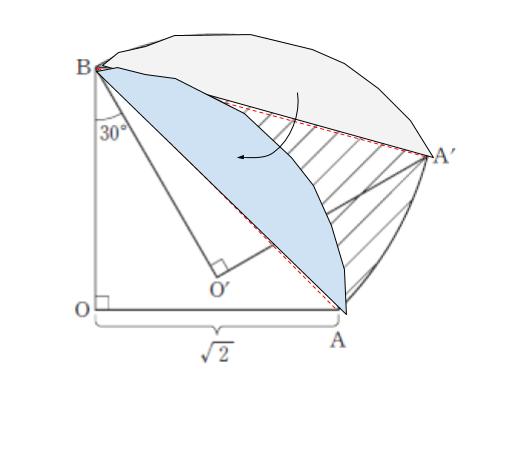
扇形 BAA’ は、半径(BA)が 2、中心角 30° の扇形です。扇形は円の一部なので、面積を求める公式は『同じ半径の円の面積×中心角/360 です』。BA の長さは、直角二等辺三角形である△OAB に注目することでわかります。2 です。半径 2 の円の面積は 4π です。従って、求める面積は 4π×30/360 = 1/3 πです。
正解は 3 です。

コメント