問 題
次のケインズ型消費関数について考える。
C = c0 (Y - T)+c1
ここで、C は消費支出、Y は総所得、T は租税(一定)、c0 、c1 は正の定数、0< c0 < 1である。このケインズ型消費関数に関する次の記述のア~ オに入るものの組合せとして妥当なのはどれか。
家計の消費支出は、総所得から租税を差し引いた ア と、所得水準に関係なく消費される基礎的消費 c1 とに基づいて決定される。
ア が1単位増加した際の消費の増加分 c0 を イ といい、縦軸に消費支出、横軸に ア をとった平面上に、線形の消費関数を描いた際の ウ に相当する。
また、ア に対する消費支出の割合を エ といい、上記の平面上においては原点と消費関数上の点を結ぶ直線の傾きに相当し、ア が大きくなるほど エ は オ。
正解 (1)
解 説
ア ですが
総所得ー租税なので「可処分所得」です。恒常所得とは、今から生涯にわたる平均可処分所得のことです。フリードマンによる恒常所得仮説における概念です。
イ ですが
「1単位増加した際の増加分」とくれば、「限界~」 です。イは「限界消費性向」です。これにより、正解は 1 or 2 です。ウ は「傾き」、エ は「平均消費性向」とわかります。
オ ですが
以下の図を考えます。可処分所得が大きくなると、原点と消費関数上の点を結んだ直線の傾きは「小さく」なります。
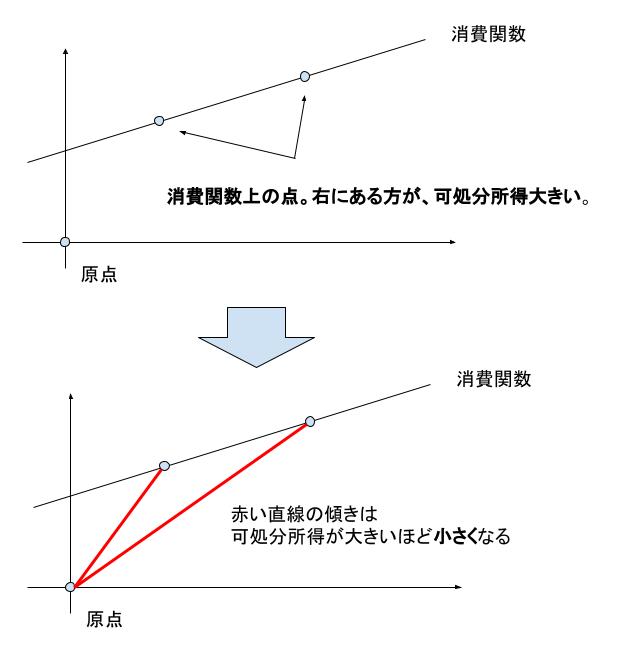
以上より、正解は 1 です。

コメント