問 題
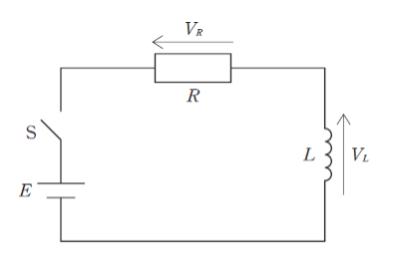
図のような RL 直列回路において,時刻 t = 0でスイッチ S を閉じてからの抵抗の両端にかかる電圧 VR とコイルの両端にかかる電圧 VL の時間変化を表したものとして最も妥当なのはどれか。

解 説
コイルが出てきたら、とにかく「コイルは変化をきらう」です。電圧がどんってかかると、「えっ、何これ、なんとかもとに戻りたい・・・」と抵抗するイメージです。VL は「だんだん下がり、限りなく 0 に近づきます」。VL がだんだん上がっている 選択肢 2,3 は誤りです。
さらに
VL と VR の和は常に E なので、時刻 t = 0 の時、VR = 0 です。これにより、選択肢 5 は誤りです。
最後に、時間が十分経過した時、VR = E に近づきます。そのため、選択肢 4 は誤りです。
以上より、正解は 1 です。
ーーー以下、完全に補足。公務員試験 技術区分 不要な内容ーーー
ちなみに、キルヒホッフの電圧則から、回路方程式と呼ばれる式を立て、電流について解けます。そこから抵抗、コイルの電圧について時間変化を求めるという解き方もあります。
この際、電流を i(t) とおけば、抵抗部分の電圧降下は R × i(t) です。コイルの両端にかかる電圧は「流れる電流の変化」に比例します。比例定数が L です。よって、コイル部分の電圧降下は L × (d/dt) i(t) です。
E = Ri(t) + L(d/dt) i(t) を、i(t) について解く方法としては2通りあります。1つは微分方程式として解く方法です。もう1つは、ラプラス変換を用いることで、四則演算の範囲で解く方法です。繰り返しますが、完全に補足です。公務員試験技術区分には不要です。
【微分方程式 解法】
i(t) = y、(d/dt) i(t) = y’ とおきます。
E = Ry + Ly’ です。y’ = dy/dt と書き直します。このパターンは、変数分離形と呼ばれます。目標となる形は 「dy/f(y) = (y 以外の文字の式ばっかり)dt」 です。

【ラプラス変換】
i(t) のラプラス変換を I(s) とおく。
E = Ri + Ldi/dt の両辺をラプラス変換する。
E/s = RI(s) + L(sI(s))となる。I(s) について解くと
I(s) = E/s(sL+R)
I(s) = E/L × 1/s(s + R/L)
部分分数分解
I(s)
= E/L × {L/R(1/s – 1/(s+(R/L))}
= E/R × (1/s – 1/(s+(R/L)) )
逆ラプラス変換より
i(t) = E/R × (1 – e(-Rt/L)) を得ます。補足終了。

コメント