問 題
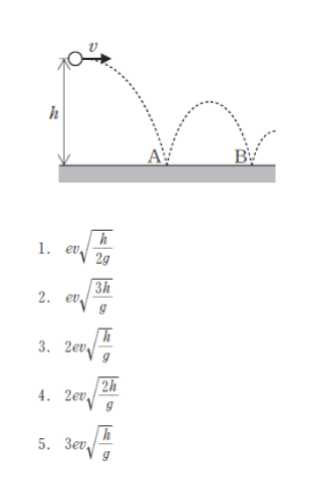
高さ h の位置から小球を初速度 v で水平に投げたところ、水平で滑らかな床の点 A に落下してはね返り、再び点 B で床に落下した。
このとき、AB 間の距離として最も妥当なのはどれか。
ただし、小球と床のはね返り係数を e、重力加速度の大きさを g とする。
解 説
初速 0 で、高さ h から自由落下した場合、床に付く瞬間の速度は √2gh 。これは知識として覚えておくとよいです。
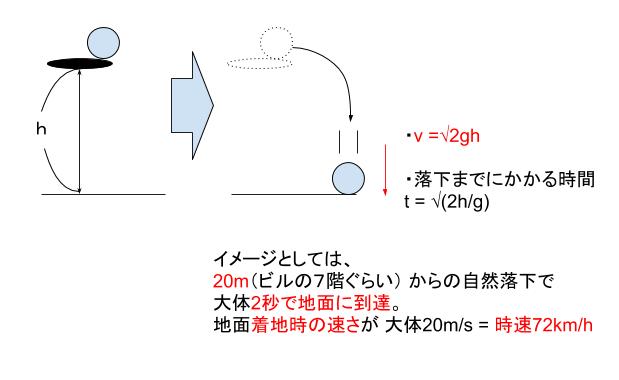
ー補足ー
ちなみになんでそうなるかというと、自由落下なので、加速度は g 。速さ 及び 変位についての基本公式が
v = at 、x = 1/2 at2
変位についての公式において、x = h、a = g を代入すれば
h = 1/2 gt2
t について解けば
t = √(2h/g)
です。
従って、v = at の右辺の a に g を、t に√(2h/g)代入すれば
v = √2gh
となります。
ー補足終わりー
求めたいのは AB 間の距離です。横向きには、ずっと v で動いているから等速直線運動と考えれば、距離は vtです。
必要なのは「Aで跳ね返ってからB に到達するまでの時間」です。以下は、縦方向に着目して考えます。
(※物理ですごく重要な基本的考え方※『真横、真縦を、それぞれだけ注目して考える。』)
はね返り係数が e と言われたら、はね返った時に速度が e 倍になると考えれば OKです。
従って、A 点において1回めの床への衝突後、上向きの速度は e√2gh 。
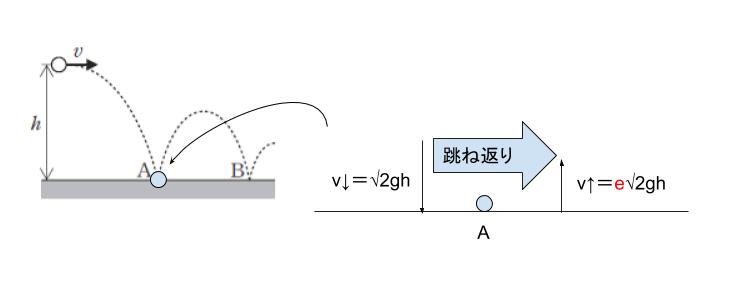
A点以降において、縦向きの速度について下向きに重力加速度があるから、初速 e√2gh、加速度下向きに g です。
つまり、A点で跳ね返った後、時間が t 秒経った時の速度はe√2gh – gt と表されます。
ここで、e√2gh -gt = 0 となるような t を考えます。
※この式における 「t」 は「縦方向の速度が 0 になるような 」t です。
いいかえると、「A で跳ね返ってから最高点に到達するまで」にかかった時間です。
t について解けば
t = e√(2h/g)
となります。この t を 2 倍すればAB間にかかった時間がわかります。すなわち 2t = 2e√(2h/g) がAB間にかかった時間です。
AB間にかかった時間がわかったのでAB間の距離がわかります。横向きに等速 v で移動しているので、v×(2e√(2h/g))がAB間の距離です。
数字と文字の順番を変えれば、2ev√(2h/g)となります。
以上より、正解は 4です。

コメント