問 題
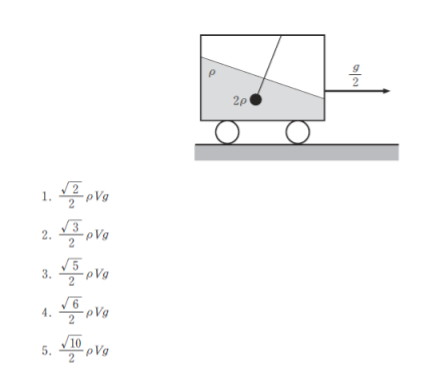
図のように、水平面上を加速度g/2で移動する台車の中において、細い糸でつり下げられた密度2ρ、体積Vの小球が密度ρの液体に浸され、台車から見ると静止している。
このとき、糸の張力の大きさとして最も妥当なのはどれか。ただし、重力加速度の大きさをgとする。
解 説
小球に注目します。本問では質量ではなく体積と密度が与えられています。質量=体積×密度 です。
従って、小球の質量は 2ρ×V = 2ρV です。質量 2ρV なので下向きに 2ρVg の力がかかります。
本問では小球が「液体の中」にいるので、浮力がかかります。F浮力=「液体の密度」×「押しのけられた液体の体積」 × g です。本問では、ρVg です。
以上より、小球には下向きに 2ρVg ーρVg = ρVg の力がかかります。
張力 T は糸の方向、つまり斜めの方向にかかるので、縦と横に分解します。
静止しているので、小球に注目すればΣ縦=0です。従って、張力の縦方向の力の大きさは、ρVg です。
ここまでを図に書き込んでまとめると下図のようになります。
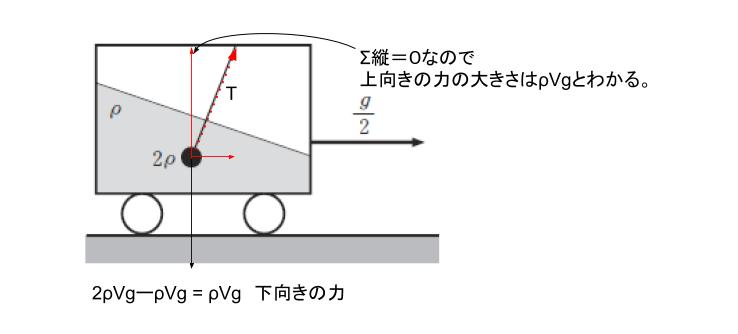
Tの横向きの力は何と釣り合っているのかというと、本問では「加速度 g/2」で移動しているという条件があるため「進行方向と逆向きに働く慣性力」と釣り合っています。
問題文に「加速度○○で移動している」ときたら、「進行方向逆向きに F慣性力=ma」 がポイントとなります。必ず思い出せるようにしましょう。
本問では小球が液体に浮いて軽くなっているので、公式の m の部分には ρV を代入します。a の部分には、g/2 を代入します。すると、慣性力は ρVg/2 です。
そして、Σ横=0なので、Tの横向きの力もρVg/2 とわかります。
求めるのはTの大きさなので、三平方の定理より
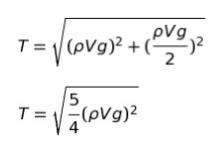
外せる √ をとれば T=√5/2 ρVg です。
従って、正解は 3 です。

コメント