公務員試験 H27年 国家一般職(土木) No.3解説

　問 題　　　　　

xy平面上において、tを媒介変数としてx=2t²＋1、y=3t²＋2t＋1で表される曲線上にある点(3,2)における接線の傾きはいくらか。

1. 1
2. 2
3. 3
4. 4
5. 5

 

 

 

 

 

　解 説　　　　　

【解法 1：パラメータ表示の微分】

接線の傾きは dy/dx です。これを（dy/dt) / (dx/dt) と考えます。

• dx/dt = 4t です。
• dy/dt = 6t+2 です。

従って、dy/dx = (6t+2)/4t・・・（１）

と表すことができます。

点（3,2）というのは、t = -1 の時の値です。（１）に、t = -1 を代入して、

-4/-4 = 1 です。

【解法 2：具体的な点を考えて推測】

解法１を知らなくても、ぜひこの問題は具体的な点から、少しでも選択肢をしぼりたい所です。

• t = 0 の時、（1,1）です。
• t = 1 の時、（3,6）です。
• t = -1 の時、（3,2）です。
  （↑これが求めたい接線の接点とわかります。）
• t = -2 の時、（9,9）です。

これらの点を、t が－２から－１，０，１と変化していったと考えて順々に滑らかにつなぐと、以下のようになります。

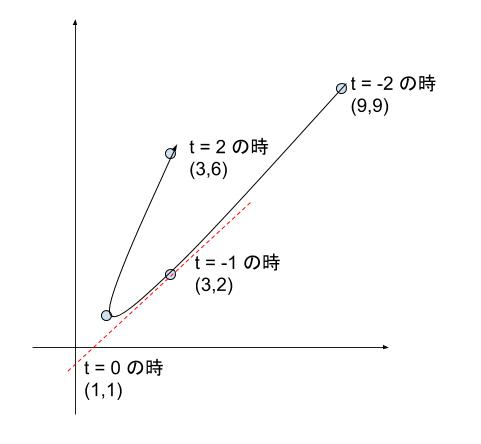
赤の点線が大雑把な接線の雰囲気となります。選択肢から、傾きの候補は 1,2,3,4,5 です。1 が一番近そうと判断できると思います。

以上より、正解は 1 です。