問 題
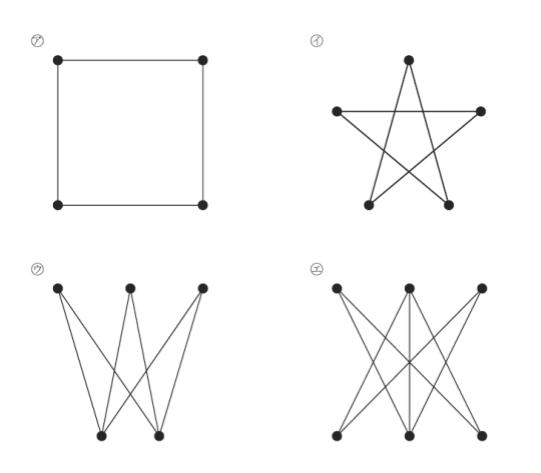
グラフ G の頂点集合を二つの素な部分集合 A と B に分割でき G の全ての辺は A の頂点と B の頂点を結んでおり、かつ、同じ部分集合に含まれる頂点どうしの間には辺が存在しないとき G は2部グラフと呼ばれる。さらに A の各頂点が B の全ての頂点と辺で結ばれているとき G は完全2部グラフと呼ばれる。次の㋐~㋓のグラフのうち完全2部グラフとして妥当なもののみを全て挙げているのはどれか。ただしグラフ中の黒丸は頂点を表している。
1. ㋐
2. ㋐ ㋒
3. ㋐ ㋓
4. ㋑ ㋓
5. ㋒ ㋓
正解 (2)
解 説
㋐について
左上から頂点に時計回り(⤵)に、1,2,3,4と番号を付けます。そして1,3の頂点と、2,4の頂点 という部分集合にわけると2部グラフです。さらに、頂点1は2,4と、頂点3は2,4と結ばれているため、㋐は完全2部グラフです。
㋒ ですが
上3つの頂点と下2つの頂点という部分集合にわけて、上3つをAと考えれば、各頂点はBの全ての頂点と辺で結ばれています。よって、㋒も完全2部です。
以上より、正解は 2 です。

コメント