問 題
秒速0.5m で動く長さ150m の動く歩道が二つ平行に設置されており、一つは甲地点から乙地点に向かって、もう一つは乙地点から甲地点に向かって動いている。Aが甲地点から動く歩道に乗りその上を秒速1.0m で歩いていたところ、甲地点を出て40秒後に反対方向から動く歩道に乗ってきたBとすれ違った。
すれ違う瞬間にBに気付いたAは、Bに追い付くため歩く速さを上げて乙地点まで行き、Bが乗っている動く歩道に乗り換えその上を乗り換える直前と同じ速さで歩いたところ、終点の甲地点でちょうどBに追い付いた。
このときBとすれ違った後のAが動く歩道の上を歩く速さはいくらか。
ただしBは動く歩道の上で歩いていないものとする。またAがBに追い付くための歩く速さは一定とし、さらにAが乙地点で動く歩道を乗り換えるために要した時間は無視するものとする。
1. 秒速1.1m
2. 秒速1.2m
3. 秒速1.5m
4. 秒速1.6m
5. 秒速1.8m
正解 (3)
解 説
秒速 0.5m で移動する動く歩道上を 秒速 1.0m で歩けば、1秒で 1.5m 進みます。従って、40 秒後には 1.5 × 40 = 60m 進んでいます。甲から 60m の地点で B と出会い、Bは歩いておらず乙→甲に向かっているので、60 ÷ 0.5 = 120 秒後に甲に着きます。
A はこの 120 秒で、90m + 150m = 240m 歩かなければならないため、240 ÷ 120 = 2m/秒の速さが必要です。
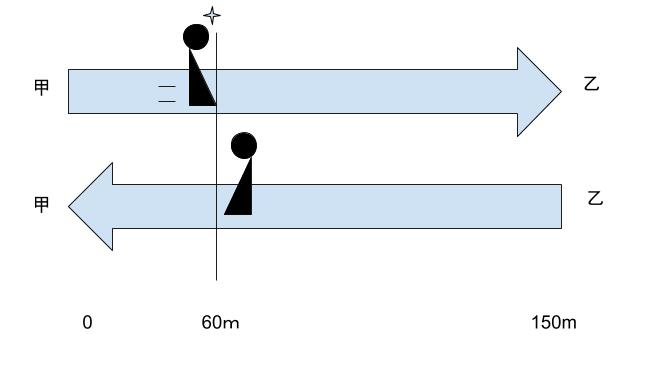
秒速 0.5m の動く歩道だから、A の歩く速さは 2 ー 0.5 = 1.5m/秒とわかります。
以上より、正解は 3 です。

コメント