問 題
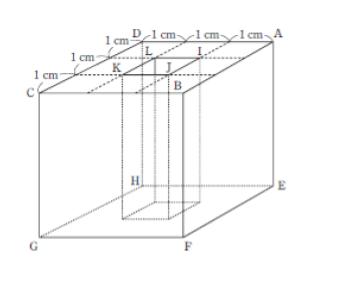
一辺の長さが3cm の立方体がありこの立方体に図のような上面から底面に貫通する直方体状の穴をあける。この立体を頂点A F Hを通る平面で切断するとき頂点Eを含む立体の体積はいくらか。なおAD とIL CD とKL はそれぞれ平行である。
1 23/6 cm3
2 4 cm3
3 25/6 cm3
4 13/3 cm3
5 9/2 cm3
正解 (4)
解 説
点A、F、Hを通る平面で切断が、まず少しイメージしづらいですね。。。
同じ平面に2点があるなら、直線で結んでOKというルールで線を引くと、以下のようになります。頂点 E を含む立体は、貫通する穴がなければ単純な三角錐であるとわかります。
さらに、結局中でくり抜かれている部分も、外側の直方体と同じように底面の正方形をすぱっと斜めに切られて、すーっと平面で切れば、同じような三角錐ができるはずと考えられます。
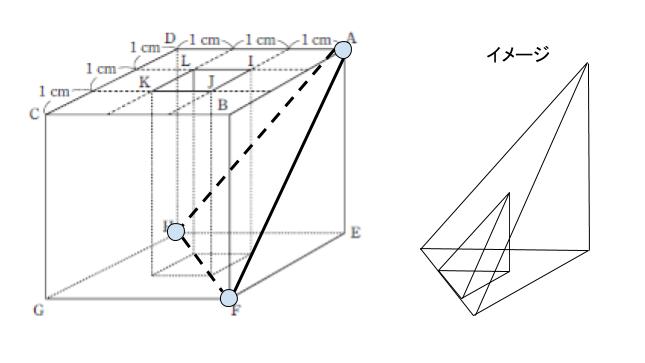
外側の大きな三角錐は、底面が 1辺 3cmの正方形のちょうど半分なので、面積は 9/2 です。高さが 3 で、錐体なので 「× 1/3」 すれば、体積は 9/2 です。
内側の小さな三角錐は、相似比が 3:1 なので、体積比は 27 : 1 のはずです。従って、小さな三角錐の体積は 大きな三角錐の 1/27 です。
9/2 × 1/27 = 1/6 です。
求めたい体積は、外側の三角錐ー小さな三角錐です。9/2 ー 1/6 = 26/6 = 13/3 です。
以上より、正解は 4 です。

コメント