問 題
図のような道路がある町において、道路を進む際、進むことのできる道路の方向が、東方向、北方向、及び北東方向の3方向に限られるとき、図のA地点からB地点を経由してC地点へ行く道順は何通りあるか。
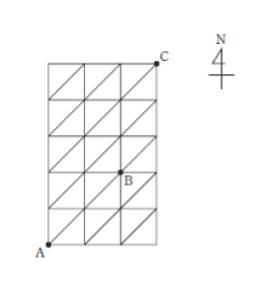
- 65通り
- 78通り
- 84通り
- 91通り
- 98通り
正解 (4)
解 説
簡単な最短経路から考えていくとよいです。
北東がない、最小の四角い区画を考えます。
A から右上の点に行くには、まず右に行くか、まず上にいくかです。それぞれ1通りしかありません。それぞれの点に、その点に行く通りを小さくメモします。
すると、A の右上の点には、1+1で2通りの行き方があります。下図のようにまとめることができます。
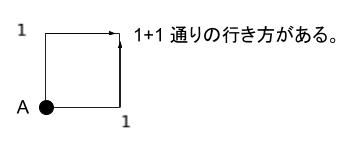
斜めもある場合、A 点は start 地点なので、この点までの通りは1通りです。その1通りを更に足す必要があります。以下のように表すことができます。

これをふまえ、A からの行き方が 1通りしかない東のみ進めば到達できる点と、北のみ進めば到達できる点に1を打ちまくり「ある点から見て左と下と左下の数値が揃ったら足す」という操作を続ければ、各点への道順がわかります。初めの方を図示すると、以下のようになります。

すると、まず B までの経路は 5 + 3 + 5 = 13 です。
また、B から C までの経路は、下図における A→C’ と同じなので 7 通りです。
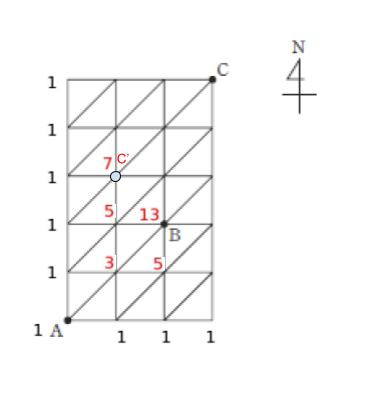
よって、A → B → C は 13 × 7 = 91 通りとわかります。
以上より、正解は 4 です。

コメント