公務員試験 H26年 国家一般職(化学) No.44解説

　問 題　　　　　

流通管型反応器に関する、次の記述の ㋐、㋑ に当てはまるものの組合せとして最も妥当なのはどれか。

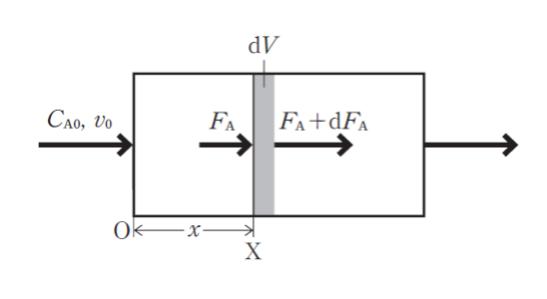
「成分Aが、反応速度 r_A〔mol/(m³・s)〕で消費される反応を流通管型反応器で行う。図は、反応体積 V〔m³〕の流通管型反応器の模式図であり、反応器入口を原点とし入口からの距離が x である位置 X における成分 A のモル流量をF_A〔mol/s〕反応率を X_A とする。

X における体積要素 dV での反応の結果、成分 A が F_A＋dF_A のモル流量で流出すると考えると、dF_A は dF_A = －r_AdV で表すことができる。また、反応器入口の流量をv₀〔m³/s〕、成分Aの初濃度をC_A0〔mol/m³〕とするとF_A = v₀C_A0(1－X_A)となる。

以上より、定常状態における流通管型反応器の空間時間 V/v₀ は、反応器出口での反応率を X_V とすると、V/v₀ = ( ㋐ )となる。また、この反応が成分Aに対する一次の発熱反応で、熱交換器により反応器内の温度がどの場所でも等しくなるように制御されている場合 ( ㋑ )。」

 

 

 

 

 

　解 説　　　　　

問題文より、dF_A = ーrAdV、F_A = v₀C_A0(1ーX_A) です。「F_A」が共通なのでとりあえず代入してみます。d{v₀C_A0(1ーX_A)} = ーrAdV　となります。選択肢より 「dX_A」が必要なので両辺を dX_A で割ってみます。

d/dX_A {v₀C_A0 ー v₀C_A0X_A} = ーrAdV/dX_A・・・（１）

すると、左辺はd/dX_A｛　｝という形なので、X_A で｛ ｝の中身を微分すると、以下のように ーv₀C_A0 だけが残ります。

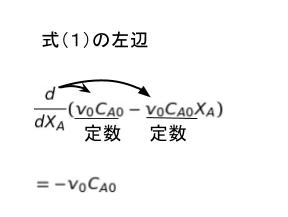
従って、式（１）は以下のように書き直せます。

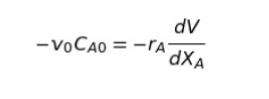
選択肢より、右辺としてありえるのは「r_AdX_A か dX_A/r_A」です。符号や dV は無視すると、右辺は今「r_A/dX_A」なので、辺辺逆数をとります。

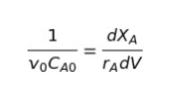
右辺を完全に dX_A/r_A とするため、両辺に dV をかけます。

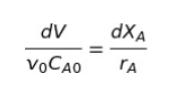
辺辺積分します。V は0→V、X_A は 0→Xv です。

 

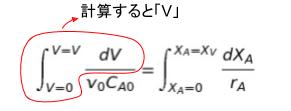
∴ V/v0 = C_A0∫ dXA/rA です。正解は 4 or 5 です。

そして、この反応が「Aに対する一次の発熱反応」とは「反応速度が A の濃度に比例する」という事です。従って、A の濃度が高いほど、反応速度が大きく、より大きな発熱がみこまれます。本問の反応は「A が消費される反応」とあるので A の濃度は「入り口側ほど大きい」と考えられます。従って、反応器「入口側」での発熱が出口側よりも大きいと判断できます。

以上より、正解は 5 です。