公務員試験 H26年 国家一般職(化学) No.43解説

　問 題　　　　　

伝熱に関する、次の記述の㋐、㋑、㋒に当てはまるものの組合せとして最も妥当なのはどれか。

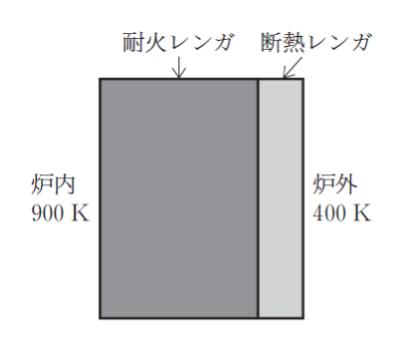
「厚さ 35.0 cm、熱伝導率 1.40 W/(m・K)の耐火レンガで囲まれた電気炉において、電気炉内部の温度 900K、炉外の温度 400K で定常伝熱となっている。このときの炉壁の熱流束は ( ㋐ ) W/m² である。

このレンガの断熱性を高めるために、図のように厚さ10.0cm、熱伝導率0.200W/(m・K)の断熱レンガを設置した。炉内と炉外の温度が、断熱レンガを設置する前と同様にそれぞれ 900 K、400 K で定常伝熱になっているとき、耐火レンガと断熱レンガの境界部の温度は ( ㋑ ) K でありこの2層レンガの熱流束は約 ( ㋒ ) W/m²となる。」

㋐　　　　㋑　　　㋒
1．125　　　733　　67
2．125　　　790　　67
3．2000　　733　　670
4．2000　　790　　670
5．2000　　790　　1700

 

 

 

 

 

　解 説　　　　　

㋐ですが
熱流束とは「熱の伝熱速度　を断面積 A で割ったもの」です。熱流束を q とおけば、q = ーλdQ/dx です。※λ = 熱伝導率です。この式は知識です。ただし単位を合わせれば忘れていても導くことができます。

本問において
dQ = -500, dx = 0.35m です。従って、q = 1.4 × 500 / 0.35 = 2000 です。正解は 3~5 です。

㋒ ですが
900K と 400K で「定常状態」というキーワードが出たので、以下のような、伝熱速度を Q_1、Q₂ とおいた図を考えます。

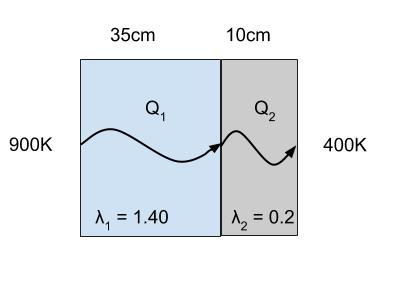
「定常状態」なので、Q₁ = Q₂ です。Q₁ = Q₂ = Q とおきます。境界の温度を T とおけば以下のような関係式（式１、式２）が成り立ちます。

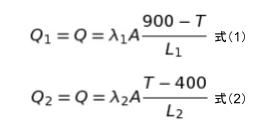
次の式は、知識として覚えた方がよいです。

定常状態において、上のように各部分において「Q = ・・・」と式を複数作った後でうまく式を代入して整理することで、Q は『分子が 「ΔT,すなわち端っこ同士の温度差」、分母が「L₁/λ₁A ＋L₂/λ₂A＋・・・と続く形」』になります。※この形を覚えておいた方がいいです！

本問で言えば、ΔT = 900-400 = 500 です。分母の方は、0.35/1.4A + 0.10/0.2A です。つまり、以下のような式になるということです。

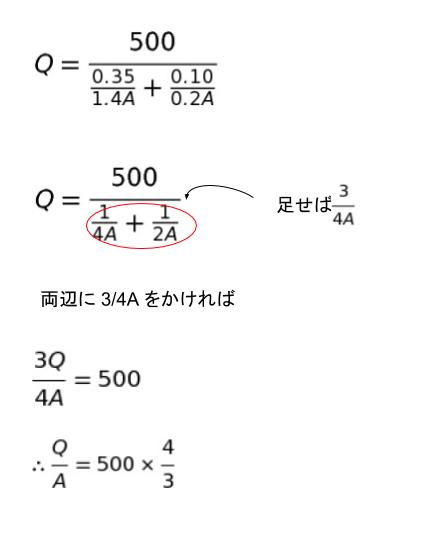
Q/A が「熱流束」です。先に㋒がわかるのですが、㋒は 約 670 となります。Q/A がわかれば、式１、式２　のどちらかの式において両辺を A で割って数値を代入すれば T がわかります。

また、意味を考えれば、熱流束をまず熱伝導率で割れば、1m あたり何度変化するかがわかります。それに長さをかければ、結局何度変化するかがわかります。

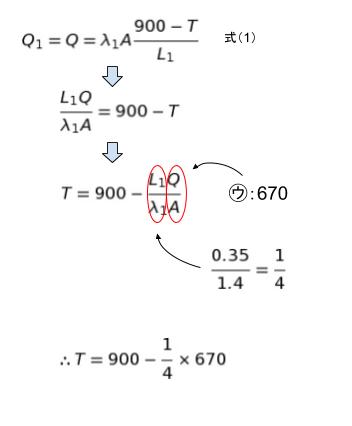
となり、T ≒ 733 です。

以上より、正解は 3 です。