問 題
図のように、質量 m の小球を付けた長さ L の糸の一端を天井に付けて、鉛直方向と糸のなす角が60°となるように小球を水平面内で等速円運動させた。このとき、この円運動の周期として最も妥当なのはどれか。ただし、重力加速度の大きさを g とする
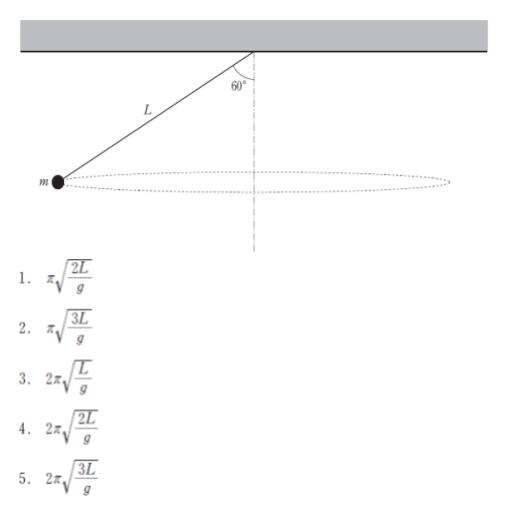
正解 (1)
解 説
【解法1 円錐振り子の周期の公式】
単振り子、ばね振り子の周期と合わせて「円錐振り子の周期」については、公式として覚えておくとよいです。単振り子の 「l」が「lcosθ」になったものです。すなわち
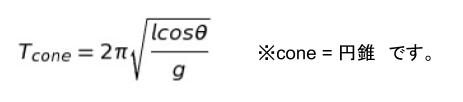
本問では θ = 60° なので、cos 60° = 1/2 です。公式に 1/2 を代入して、解答の選択肢に形を合わせると以下のようになります。
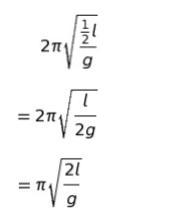
以上より、正解は 1 です。
【解法2 等速円運動に注目】
等速円運動という点に着目してまず思い出す公式は、遠心力 = mrω2 です。力の釣合いを考えると以下のようになります。
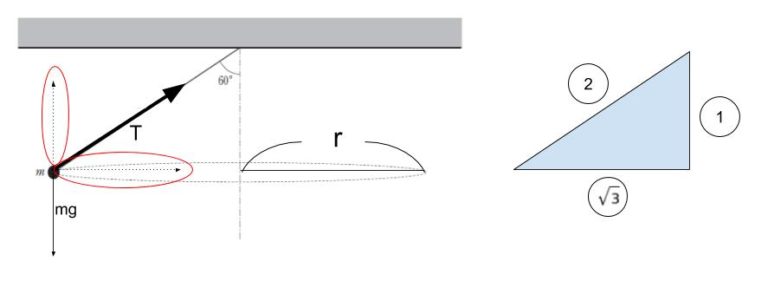
張力 T を縦に分解したもの(赤丸囲い)は、縦方向の力の釣合に注目すれば mg とわかります。
一方、張力 T を横に分解したもの(赤丸囲い)は、特殊な直角三角形の辺の比より√3mg とわかります。この力は遠心力と釣り合うはずです。遠心力の公式に含まれる「r」は、L を含む直角三角形に注目すれば、辺の比から √3/2 L と表されます。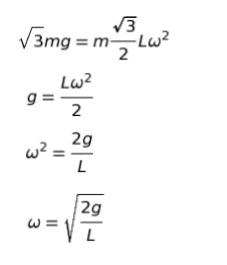
となります。ω とは、角速度です。1 秒間に何ラジアン進むかです。そして、1 周が 2πラジアンです。よって、周期、つまり「1周に何秒かかるか」は「2π ÷ ω」 で求めることができます。
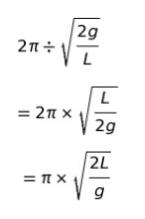
となり、正解は 1 です。

コメント