問 題
碁石を使って次のような操作を行うことを考える。
① 正方形の枠に沿って枠内に碁石を並べる。(並べた碁石の内側には碁石を置かない。)
② 並べた碁石の四つの辺のうち左側の一辺を残して碁石を取り除き取り除いた碁石を残した一辺の右側にそろえて並べていく。一辺の数に満たない数の碁石が残った場合、残した一辺の右側に下からそろえて並べこれを最後の列の碁石とする。
以上の操作を例えば一辺に5個の碁石を用いて行うと下図のようになる。
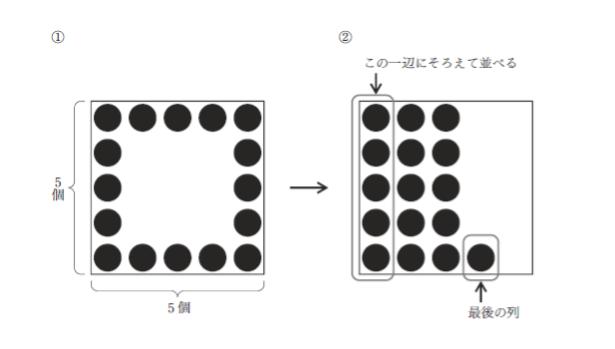
A B Cの3人がそれぞれ操作を行った結果、人が使用した碁石の総数は96個となり、最後の列の碁石の個数を見るとAは5個Bは3個となった。このときCが並べた正方形の一辺当たりの碁石の個数はいくつか。
- 8個
- 9個
- 10個
- 11個
- 12個
解 説
わけのわからないパターンなので、具体的に考えます。一辺5個の場合を図で与えてくれているので、図を見て考えると、操作①では、5×5の碁石から、3×3の碁石を取り除いていると考えることができます。
従って、1辺に n 個の碁石を用いたとすると n2 ー (n-2)2 = 4n ー 4 個の碁石を操作①で使っています。
操作 ② では、 n 個ずつ並べているので、「n で割った余り」が最後の列の碁石になっています。後は、具体的に n に数値を代入していけば、見通しが立ちそうです。
n = 3 → 碁石 8 個使って、最後の列の碁石 は 2個です。n = 4 → 碁石 12個使って、最後の列の碁石は 4個です。これらは、A、Bの用いた碁石の個数ではありません。
n = 6 以降を引き続き具体的に考えてみると
- n = 6 → 20 個の碁石を使い、最後の列の碁石は 2個で、ダメ。
- n = 7 → 24 個の碁石を使い、最後の列の碁石は 3 個。これは B か?
- n = 8 → 28 個の碁石を使い、最後の列の碁石は 4 個。ダメ。
- n = 9 → 32 個の碁石を使い、最後の列の碁石は 5 個。これは A か ?
仮に B が 24個、A が 32個の碁石を使ったとすると、総数 96 個であれば、残りは 40 個です。4n ー 4 = 40 → n = 11 となります。選択肢から、C の一辺は 8~12 なので、妥当です。
以上より、正解は 4 です。

コメント