問 題
現金通貨を C、預金通貨を D としたとき、現金預金比率 (C/D) が 0.2、法定準備率が 0.3でいずれも常に一定であるとする。また、銀行の支払準備と法定準備は一致しており、銀行の手元保有現金がゼロであるとするとき、次の記述のうち、妥当なのはどれか。
1. 通貨乗数(貨幣乗数)は3となる。
2. ハイパワード・マネーを 10 兆円増やしたとき、預金通貨は 20 兆円増える。
3. ハイパワード・マネーを 10 兆円増やしたとき、現金通貨は8兆円増える。
4. ハイパワード・マネーを 10 兆円増やしたとき、マネーストックは 40 兆円増える。
5. ハイパワード・マネーが 200 兆円のときのマネーストックは、640 兆円である。
解 説
貨幣市場に関する問題です。基本的な知識として、マネーサプライを M とした時、M = C+D です。C は現金、D は預金です。すなわち、マネーサプライは、家計・企業の有する現金+預金です。また、日銀が所有する現金や準備金を、ハイパワードマネーといい、H で表します。H = C+R です。C は現金、R は準備金です。そして、M = ◯ × H という形に表した時の「◯」を貨幣乗数といいます。
選択肢 1 ですが
貨幣乗数を◯とすると、M = ◯ × H です。従って、◯ = M/H です。M/H を計算すると、(C+D)/(C+R) です。与えられた C/D を用いるために、分母・分子を D で割ります。ちなみに「法定準備率」は、銀行が預金に対して準備する準備金の割合です。R/D です。以下のように計算できます。
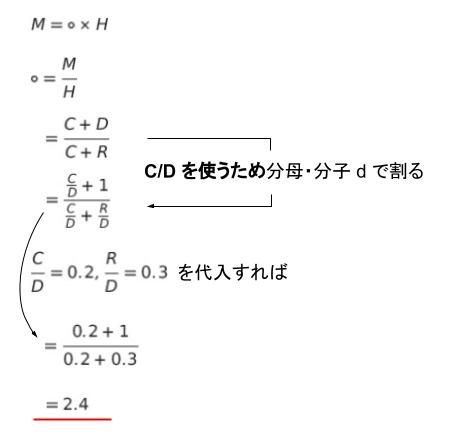
貨幣乗数は 2.4 です。3 ではありません。選択肢 1 は誤りです。
選択肢 2 は妥当です。
選択肢 1 より貨幣乗数が 2.4 なので、H を 10 兆円増やせば、M が 24 兆円増えます。そして、現金預金比率 0.2 なので、比を考えると、「現金が①増えた場合、預金が⑤増えます。全体として⑥増え」ます。すると、M が 24 兆円増えた場合、現金が 4 兆円、預金が 20 兆円増えます。
選択肢 3 ですが
H を 10 兆円増やした場合、増える現金は 4 兆円です。選択肢 3 は誤りです。
選択肢 4 ですが
H を 10 兆円増やした場合、増える M は 24 兆円です。40 兆円ではありません。選択肢 4 は誤りです。
選択肢 5 ですが
H が 200 兆円のとき、M = 480 兆円です。640 兆円ではありません。選択肢 5 は誤りです。
以上より、正解は 2 です。

コメント