公務員試験 H26年 国家一般職(行政) No.35解説

　問 題　　　　　

ある財を独占的に供給する独占企業の直面する市場需要関数が、x ＝ 120－ p で示されるとする。またその独占企業の総費用関数が c = x² で示されるとする。ここで、x は数量、p は価格、c は総費用である。独占均衡においてラーナーの独占度(需要の価格弾力性の逆数と等しい。)はいくらか。

1.1/3
2.1/2
3. 1
4. 2
5. 3

 

 

 

 

 

　解 説　　　　　

独占均衡とは、利潤を最大化する価格と数量です。利潤＝売上ー費用です。売上 ＝ 価格 × 個数です。売上は px です。x = 120 – p とあるので、代入すると、p(120 – p) と表すことできます。費用が x² とあります。x = 120 – p を代入すると、費用は (120 – p)²  です。従って、利潤は f(p) = p(120 – p) – (120 – p)² と表せます。 この関数の最大値を求めます。すなわち、微分して 0 になる p を計算します。

まず、f(p) を整理すると、以下のように、f(p) = -2p² +360p – 120² となります。

 

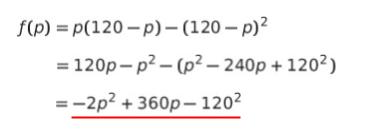
f(p) を微分すると、f’(p) = -4p + 360 です。f’(p) = 0 を解くと、p = 90 です。p = 90 の時、x = 120 – p より、x = 30 です。(x,p) = (30,90) が、独占均衡における数量と価格です。

需要の価格弾力性とは、価格が 1% 上昇した時、需要量が何％ 減少するかを表す値です。価格の 1% を考えると小数でわかりにくいため、10% 上昇させてみます。独占均衡における価格が 90 なので、10% 上昇させて、価格を 99 としてみます。すると、x は 30 → 21 となります。量が 30% 減少です。価格 10% 上昇で、量が 30% 減少なので、価格 1% 上昇に対して、量が 3% 減少です。価格弾力性は 3 です。逆数は 1/3 です。

以上より、正解は 1 です。