問 題
第1財の消費量を x1 、第2財の消費量を x2 とし、これら2種類の消費財からなる効用関数が与えられている。第1財の価格を p1 = 2、第2財の価格を p2 = 4、所得を I = 50として、この I が全て第1財及び第2財に支出されているものとする。このとき、消費者が効用を最大化して行動した場合、ア~エの記述のうち、妥当なもののみを全て挙げているのはどれか。
ア. 効用関数が u = x1 (2x2 + 5) であれば消費量の組合せは (x1 ,x2) = (5, 10)となる。
イ. 効用関数が u = x1 (2x2 + 5) であれば貨幣の限界効用は7.5となる。
ウ. 効用関数が u = min(x1 , 3x2) であれば消費量の組合せは (x1 ,x2) = (15, 5)となる。
エ. 効用関数が u = x1 + 3x2 であれば消費量の組合せは (x1 ,x2) = (25, 0)となる。
1. ア、イ
2. ア、ウ
3. ア、エ
4. イ、ウ
5. ウ、エ
解 説
具体的に考えると、1 個 2 円の第1財(りんご)を x1 個、1個4円の第2財(みかん)を x2 個購入する。その時の喜びが、x1、x2 を変数とする二変数による効用関数で表される。50円を使って効用を最大化する消費者がいる。という設定です。以下、二変数を x,y と表記します。
記述 ア ですが
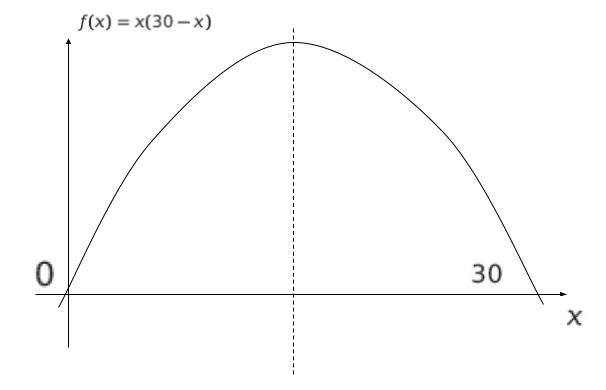
効用関数が f(x,y) = x(2y + 5) という仮定です。予算制約が 2x + 4y = 50 と表されます。両辺を 2 で割って、制約が x + 2y = 25 です。効用関数に 2y = 25 – x を代入すれば、f(x) = x(30 -x) と表せます。これは、x = 0,30 を通る上に凸の二次関数なので、グラフをかけば以下の通りです。グラフから、効用関数の最大値は x = 15 の時とわかります。ちなみに、x = 15 から y,及び 効用を求めてみると、y = 5,効用 = 225 です。
記述 ア で提示された消費量の組み合わせである x = 5,y = 10 について検討すると、効用は 5 × 25 = 125 です。効用最大ではありません。従って、記述 ア は誤りです。正解は 4 or 5 です。また、選択肢より、ウ は妥当とわかります。
記述 エ に注目すると、 極端な例として、予算制約を満たすような範囲で y 最大の場合を考えます。すなわち、x = 0、y = 12.5 を考えます。効用関数を x,y を用いて書き直せば、f(x,y) = x + 3y です。x = 0、y = 12.5 を代入すれば、効用が 37.5 となります。x = 25、y=0 の時の効用は 25 です。従って、(x,y) = (25,0) の時よりも効用が大きくなる場合が見つかりました。記述 エ で提示された消費量の組み合わせは、効用最大ではありません。従って、記述 エ は誤りです。
以上より、正解は 4 です。
ちなみに、記述 イ についてですが
貨幣の限界効用とは、効用が最大化されるような x,y 、すなわち均衡点において、step1:限界効用をどちらかの文字で微分、step2:微分した財の価格で割る という 2 ステップで求めることができます。
本問題の記述 イ であれば、均衡点 (15,5) 、効用関数を x,y どちらかで微分→結果に均衡点の数値代入→偏微分した変数の価格で割る。という流れです。一例として、x で微分する場合、以下のように計算します。y で微分していっても同じ値が出てきます。

※効用関数を u = x(2y+5) と表現しています。「du/dx」は「u を x で微分する」、「du/dy 」は「u を y で微分する」という意味です。均衡点は(x,y) = (15,5) です。記述 イ も確実に正誤判断できるようにしておくとよいです!

コメント