H26年 国家一般職(高卒 技術) No.66 土木基礎力学　解説

　問 題　　　　　

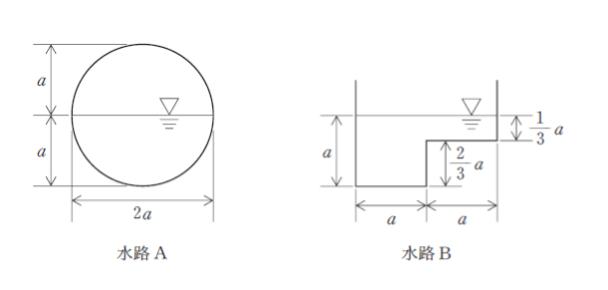
図のような断面の水路 A B における径深 R_A、R_B と平均流速 v_A,v_B の大小関係として最も妥当なのはどれか。ただし水路 A と B は両方とも同じ流量の水が流れているものとする。

 

 

 

 

 

　解 説　　　　　

流積（水路断面において流水の占める面積）A、潤辺（水路断面において水が接する長さ）S を用いて、径深 R は、R = A/S です。径深は、水理学的平均水深とも呼ばれます。

水路 A の流積は 半径 a の半円なので πa²/2 です。径深は 半径 a の半円の円周なので πa です。
水路 B の流積は 一辺 a の正方形＋辺の長さが a,a/3 の長方形 なので 4a²/3 です。径深は 4a です。
従って R_A = a/2、R_B = a/3 です。R_A > R_B となります。

平均流速については、「流量が同じ」とあるので、流量が関係する基本知識である 「Q = Av」 を思い出します。
Q = (πa²/2) × v_A です。
また、水路 B に注目すれば Q = (4a²/3) × v_B です。
π≒3.14 なので π/2 > 4/3 です。すると Q が同じなので v_A < v_B とわかります。

以上より、正解は 3 です。