問 題
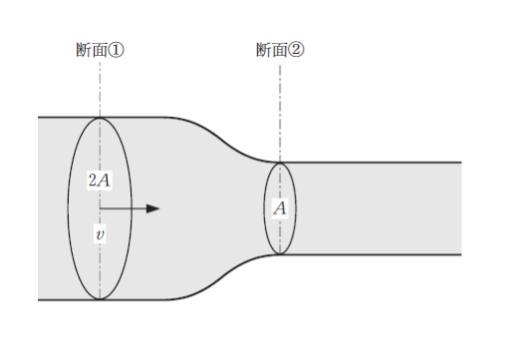
図のように水平な管路を一定流量の非圧縮非粘性流体が流れている。断面 ① における管路の断面積を 2A、流体の流速を v とし、断面 ② における管路の断面積を A とするとき断面 ② における流体の流速として最も妥当なのはどれか。
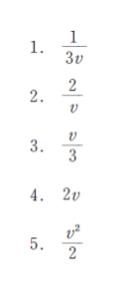
正解 (4)
解 説
断面積と流速が出てきたので「連続の式」を思い出します。Q = AV がどこでも成立します。流量は一定です。
断面①で連続の式より「Q = (2A)v」です。
次に断面②で、流速を x とすれば「Q = Ax」です。2つの式を連立すれば x = 2v とわかります。
以上より、正解は 4 です。

コメント