問 題
図のように一定量の理想気体を変化させるとき、ΔQ=Q1-Q3 及び Q2の組合せとして最も妥当なのはどれか。
ただし、図の斜線部の面積をSとする。
また、定積加熱過程(状態A→B)において気体が受け取る熱量をQ1、等温膨張過程(状態B→C)において気体が受け取る熱量をQ2、定圧放熱過程(状態C→A)において気体が放出する熱量をQ3とする。
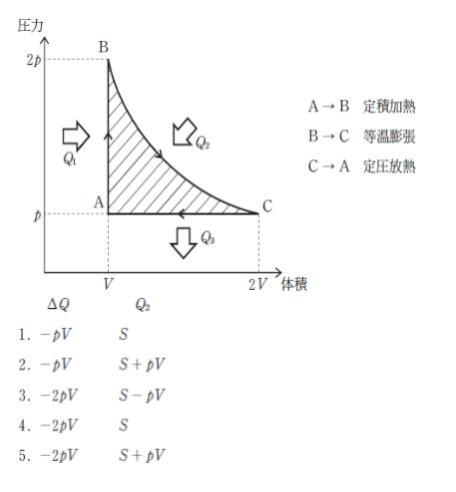
正解 (2)
解 説
理想気体と来たらまずは PV = nRTです。
サイクルで熱が出てきたら
- U=Q+W。
- U=3/2 nRT(単原子理想気体の場合)
をまず思い出してそこから考えます。
また、P-Vグラフでは囲まれた部分が「気体が外部にした仕事」 です。内部エネルギーU は温度のみで決まるパラメータです。
本問においてA→B→C→Aとサイクルを一周すると同じ状態に戻っているため、同じ温度です。内部エネルギーの変化は0です。
すると、
ΔUtotal=Qtotal+wtotal
※ w は気体が「された」仕事。
本問では、ΔU=0、w = ーS です。
従って、
Qtotal = Sとなります。
※本問で注意しなければならないのはQ1ーQ3をΔQと名付けられている点です。ちょっと紛らわしいですね。。。そこで、サイクル全体を見ている時には添字でtotal をつけています。
Qtotal というのはQ1+Q2ーQ3 のことです。順番を変えれば「Q1ーQ3」 + 「Q2」 となります。つまり、ΔQ + Q2 です。
選択肢を見ると、足してちょうど S になるのは選択肢 2 のみです。
よって、正解は 2 です。

コメント