問 題
図のように、△ABC、△DEF及び直線BF上の線分CEに接する円の半径rを、Lを用いて表したものとして正しいのはどれか。
ただし、AB:BC:CA=4:3:5、DE:EF:FD=5:3:4とし、CEの長さをLとする。

正解 (3)
解 説
そのままの図形を見てもよくわからないので、補助線を引いて考えます。
補助線を引く時の原則は
- 円が出てきたら中心と特徴的な点を結んで見る
- 直線を延長してみる
です。以下のような補助線をひいたとします。
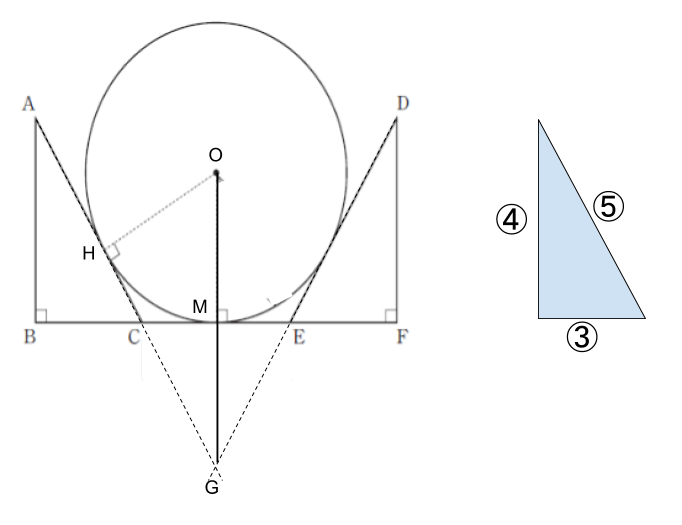
図形における三角形は全て相似で、辺の比が3:4:5です。△OHG に注目するとOH:OGが3:5です。そして、OH=OM=rです。
比で言う ③ が 長さ r なので、MG は比で言う ② とわかります。r を用いて表すと、2r/3 です。図に書き込むと、以下になります。
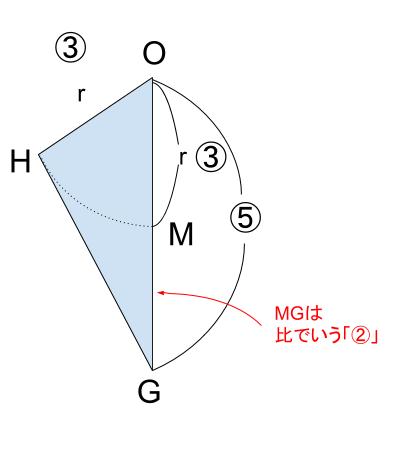
△MGCに注目すれば、やはり辺の比は3:4:5です。従って、MCの長さはMG×3/4 です。2r/3 ×3/4 = r/2 となります。CEの長さ(L)は明らかにMCの2倍なので r です。
以上より、L = r です。
正解は 3 です。

コメント