公務員試験 H26年 国家一般職(電気・電子・情報) No.40解説

　問 題　　　　　

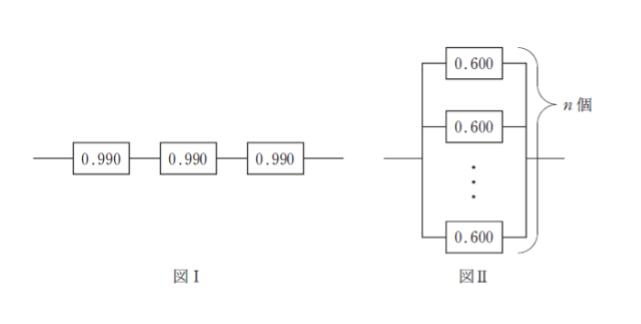
図Ⅰは、信頼度0.990 の構成要素が３個直列に接続されたシステムである。図Ⅱは、信頼度0.600の構成要素が n 個並列に接続されたシステムである。図 Ⅱ のシステムの信頼度を図Ⅰのシステムの信頼度より大きくするために必要な n の最小値はいくらか。

1. 1
2. 2
3. 3
4. 4
5. 5

 

 

 

 

 

　解 説　　　　　

選択肢から、n = 1 ~ 5 です。

図Ⅰのシステムの信頼度は 0.99 × 0.99 × 0.99 ≒ 0.97 です。

n = 1 の時、図Ⅱのシステムの信頼度は 0.6 です。
n = 2 の時、図Ⅱのシステムの信頼度は 1-(0.4)² = 1- 0.16 = 0.84 です。
n = 3 の時、図Ⅱのシステムの信頼度は 1-(0.4)³ = 1- 0.064 = 0.936 です。
n = 4 の時、図Ⅱのシステムの信頼度は 1-(0.4)⁴ = 1- 0.0256 = 0.9744 > 0.97 です。

従って、最小値は 4 とわかります。

以上より、正解は 4 です。